Tập hợp. Phần tử của tập hợp

I. Lý thuyết

1. Phần tử của tập hợp

Ví  dụ: A là tập hợp các số tự nhiên nhỏ hơn 4

Các số 0,1,2,3 là các phần tử của tập hợp

Kí hiệu: \(1\; \in A\) đọc là 1 thuộc A hoặc 1 là phần tử của A

             \(5 \notin A\) đọc là 5 không thuộc A hoặc 5 không là phần tử của A

2. Cách viết một tập hợp

Để viết 1 tập hợp, thường có 2 cách:

+  Liệt kê các phân tử của tập hợp

Ví dụ, \(A{\rm{ }} = {\rm{ }}\left\{ {0;1;2;3;4} \right\}\), \(B = {\rm{ }}\left\{ {a;b;c} \right\}\)

+ Chỉ ra tính chất đặc trưng cho tập hợp

\(A = \{ x \in N|x < 5\} \), N là tập hợp các số tự nhiên

Tính chất đặc trưng cho các phần tử x của tập hợp A đó là \(x \in N\)và \(x < 5\)  

 Lưu ý:

-        Các phần tử được viết trong dấu { }.

-         Các phần tử được liệt kê một lần không kể thứ tự liệt kê

-        Các phần tử cách nhau bởi dấu “;”

Minh họa tập hợp bằng 1 vòng kín được gọi là biểu đồ ven.

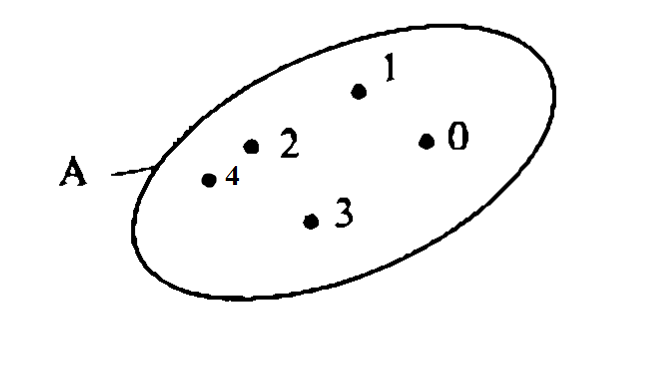
 3.    Mối quan hệ giữa các tập hợp

- Tập hợp con

Khái niệm: Nếu mọi phần tử của tập hợp A đều thuộc tập hợp B thì tập hợp A là con của tập hợp B

Kí hiệu \(A \subset B,B \supset A\)

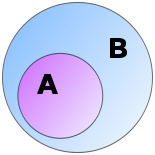
- Hai tập hợp bằng nhau nếu \(A \subset B,B \subset A\) thì A=B

- Giao của 2 tập hợp

Khái niệm: giao của 2 tập hợp A và B là 1 tập hợp gồm các phần tử chung của 2 tập hợp đó

Kí hiệu \(A \cap B\)

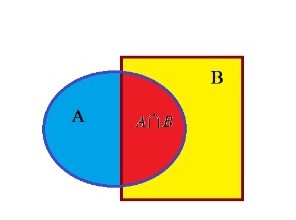
4.    Một số tập hợp thường gặp

- Tập hợp số tự nhiên

Kí hiệu N:  \(N{\rm{ }} = {\rm{ }}\left\{ {0;1;2;3;4 \ldots } \right\}\)   

- Tập hợp số tự nhiên khác 0

Kí hiệu \(N* = {\rm{ }}\left\{ {1;2;3;4 \ldots } \right\}\)

- Tập hợp rỗng

Tập hợp số tự nhiên sao cho x+10=8 là tập hợp rỗng ( không có x thỏa mãn)

Tập hợp rỗng kí hiệu là \(\emptyset \)

Lưu ý: một tập hợp có thể có 1 phần tử, nhiều phần tử, vô số phần tử (tập hợp số tự nhiên N) hoặc không có phần tử nào (tập hợp rỗng)

II.  Bài tập

Dạng 1: Viết 1 tập hợp

Hãy viết các tập hợp sau bằng 2 cách

a,Viết tập hợp A các số tự nhiên nhỏ hơn 15

b,Viết tập hợp B các số tự nhiên lớn hơn 6 nhỏ hơn 10

Lời giải:

a, cách 1: liệt kê các số tự nhiên nhỏ hơn 15

\(A = {\rm{ }}\left\{ {0;1;2;3;4;5;6;7;8;9;10;11;12;14;13} \right\}\)

Cách 2: tính chất chung của tập hợp

\(A = \{ x \in N|x < 15\} \)

b, cách 1: \(B{\rm{ }} = {\rm{ }}\left\{ {7;8;9} \right\}\)

 Cách 2: \(B = {\rm{ }}\{ x \in N|6 < x < 10\} \)

Dạng 2: phần tử của tập hợp, tập hợp con, giao của 2 tập hợp

Bài 1: Cho \(C = {\rm{ }}\left\{ {a,b,c} \right\}.\)Viết số tập hợp con của tập hợp mà mỗi tập hợp con đó có 2 phần tử

Lời giải:

TH1: tập hợp có chứa phần tử a là {a;b}; {a;c}

TH2: tập hợp có chứa phần tử b và không chứa a: {b;c}

TH3: tập hợp có chứa phần tử c – trùng với các trường hợp trên

Vậy tập hợp con của C có 3 phần tử là {a;b}; {a;c}; {b;c}

Bài 2: Tìm giao của 2 tập hợp A và B biết rằng

A= {5;7}   ,   B = {4,5,6,7}

Lời giải:

\(A \cap B = {\rm{\{ }}5;7\} \). Tập hợp A là con của tập hợp B