Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác (Phần 3)

QUAN HỆ GIỮA BA CẠNH CỦA MỘT TAM GIÁC.

BẤT ĐẲNG THỨC TAM GIÁC (PHẦN 3).

II/ Bài tập vận dụng (tiếp)

Dạng 3: Chứng minh bất đẳng thức về độ dài

Phương pháp:

Sử dụng bất đẳng thức tam giác và các biến đổi về bất đẳng thức. Chú ý đến các phép biến đổi sau:

+ Cộng cùng một số vào hai vế của bất đẳng thức:

\(a > b \Rightarrow a + c > b + c.\)

+ Cộng từng vế hai bất đẳng thức cùng chiều:

\(\left. \begin{array}{l}a < b\\c < d\end{array} \right\} \Rightarrow a + c < b + d.\)

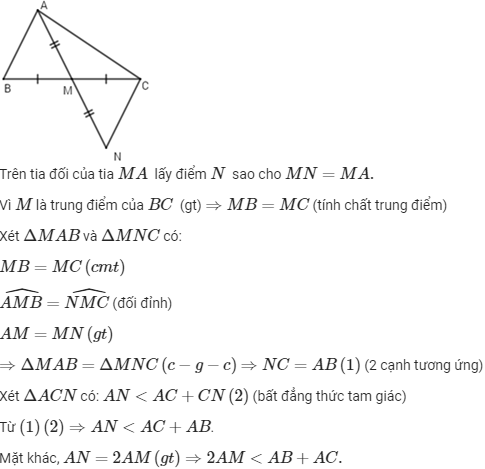
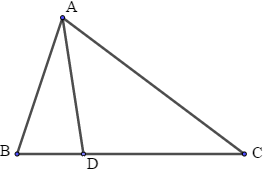
Bài 8: Cho tam giác ABC có M là trung điểm của BC. So sánh AB + AC và 2AM.

Phương pháp giải:

+ Kẻ thêm hình: Trên tia đối của tia MA lấy điểm N sao cho MN = MA.

+ Áp dụng bất đẳng thức tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kỳ lớn hơn độ dài cạnh còn lại.

Lời giải:

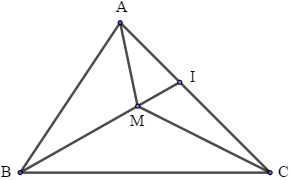
Bài 9: Cho tam giác ABC và M là một điểm nằm trong tam giác. Gọi I là giao điểm của đường thẳng BM và cạnh AC

a) So sánh MA với MI + IA, từ đó chứng minh MA + MB < IB + IA.

b) So sánh IB với IC + CB, từ đó chứng minh IB + IA < CA + CB.

c) Chứng minh bất đẳng thức MA + MB < CA + CB.

Phương pháp giải:

Áp dụng bất đẳng thức tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kỳ lớn hơn độ dài cạnh còn lại.

Lời giải:

Bài 9: Cho tam giác ABC và M là một điểm nằm trong tam giác. Gọi I là giao điểm của đường thẳng BM và cạnh AC

a) So sánh MA với MI + IA, từ đó chứng minh MA + MB < IB + IA.

b) So sánh IB với IC + CB, từ đó chứng minh IB + IA < CA + CB.

c) Chứng minh bất đẳng thức MA + MB < CA + CB.

Phương pháp giải:

Áp dụng bất đẳng thức tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kỳ lớn hơn độ dài cạnh còn lại.

Lời giải:

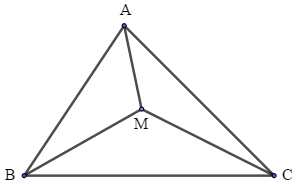
Trong ΔAMB, ta có:

MA + MB > AB (bất đẳng thức tam giác) (1)

Trong ΔAMC, ta có:

MA + MC > AC (bất đẳng thức tam giác) (2)

Trong ΔBMC, ta có:

MB + MC > BC (bất đẳng thức tam giác) (3)

Cộng từng vế (1), (2) và (3), ta có:

MA + MB + MA + MC + MB + MC = AB + AC + BC

\( \Leftrightarrow \) 2(MA + MB + MC) > AB + AC + BC

Vậy MA + MB + MC > (AB + AC + BC) / 2. (đpcm).

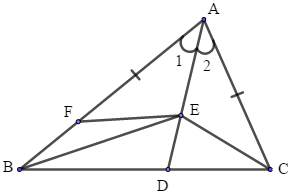
Bài 11: Cho tam giác ABC có AB > Ac, tia phân giác của góc A cắt BC ở D. Trên đoạn thẳng AD lấy điểm E. Chứng minh rằng: AB – AC > EB – EC.

Phương pháp giải:

Áp dụng hệ quả của bất đẳng thức: Trong một tam giác, một cạnh bất kì luôn lớn hơn hiệu độ dài hai cạnh còn lại và lớn hơn tổng độ dài hai cạnh còn lại.

Lời giải:

Vì AB > AC (gt) nên trên AB lấy điểm F sao cho: AF = AC.

Xét tam giác AEF và tam AEC có:

\(\begin{array}{l}\angle {A_1} = \angle {A_2}\,\,\left( {gt} \right)\\AF = AC\\AE\,\,chung\\ \Rightarrow \Delta AEF = \Delta AEC\,\,\left( {c - g - c} \right)\\ \Rightarrow EF = EC.\end{array}\)

Xét tam giác BEF, theo bất đẳng thức tam giác ta có:

BF < BE – EF, mà BF = AB – AF

Nên AB – AF < BE – EF

Mặt khác: AF = AC; EF = EC

Do đó: AB – AC < BE – EC. (đpcm).

Bài 12: Cho điểm D nằm trên cạnh BC của tam giác ABC. Chứng minh rằng:

\(\frac{{AB + AC - BC}}{2} < AD < \frac{{AB + AC + BC}}{2}.\)

Phương pháp giải:

+ Áp dụng bất đẳng thức tam giác.

+ Cộng từng vế hai bất đẳng thức cùng chiều.

Lời giải:

Xét tam giác ABD, theo bất đẳng thức tam giác ta có:

AD > AB – BD     (1)

Xét tam giác ADC, theo bất đẳng thức tam giác ta có:

AD > AC – DC     (2)

Cộng từng vế của (1) và (2) ta có:

2AD > AB + AC – (BD + DC)

Hay 2AD > AB + AC – BC

\( \Rightarrow AD > \frac{{AB + AC - BC}}{2}.\)

Chứng minh tương tự ta có:

AD < AB + BD và  AD < AC + DC

Suy ra: 2AD < AB + AC + (BD + DC)

Hay 2AD < AB + AC + BC

\( \Rightarrow AD < \frac{{AB + AC + BC}}{2}.\)

Vậy \(\frac{{AB + AC - BC}}{2} < AD < \frac{{AB + AC + BC}}{2}.\)  (đpcm).

Dạng 4: Tìm giá trị nhỏ nhất của tổng hai độ dài

Phương pháp:

+ Với ba điểm M, B, C bất kì ta có: \(BM + MC \ge BC.\)

Dấu “=” xảy ra khi và chỉ khi M thuộc đoạn BC.

+ Như vậy, nếu độ dài đoạn BC không đổi thì tổng BM + MC nhỏ nhất bằng BC khi và chỉ khi M thuộc đoạn BC.

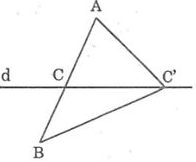
Bài 13: Cho hai điểm A và B nằm về hai phía của đường thẳng d. Tìm điểm C thuộc đường thẳng d sao cho tổng AC + CB là nhỏ nhất.

Phương pháp giải:

+ Vẽ thêm điểm phụ.

+ Áp dụng bất đẳng thức tam giác.

Lời giải:

Giả sử C là giao điểm của đoạn thẳng AB với đường thẳng d.

Vì C nằm giữa A và B nên ta có:

AC + CB = AB (1)

Lấy điểm C' bất kỳ trên d (C' ≠C)

Nối AC', BC'

Sử dụng bất đẳng thức trong tam giác vào ∆ABC', ta có:

AC' + BC' > AB (2)

Từ (1) và (2) suy ra:

AC' + C'B > AC + CB.

Vậy C là điểm cần tìm.

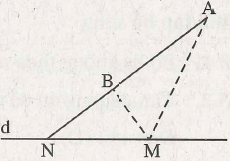
Bài 14: Cho đường thẳng d và hai điểm A, B nằm cùng một phía của d và AB không song song với d. Một điểm M di động trên d. Tìm vị trí của M sao cho |MA – MB| là lớn nhất.

Phương pháp giải:

Áp dụng bất đẳng thức tam giác.

Lời giải:

Vì AB không song song với d nên AB cắt d tại N.

Với điểm M bất kì thuộc d mà M không trùng với N thì ta có tam giác MAB. Do đó :

|MA – MB| < AB. khi M = N thì

|MA – MB| = AB.

Vậy |MA – MB| lớn nhất là bằng AB, khi đó M = N là giao điểm của hai đường thẳng d và AB.

Dạng 5: Bài toán thực tế

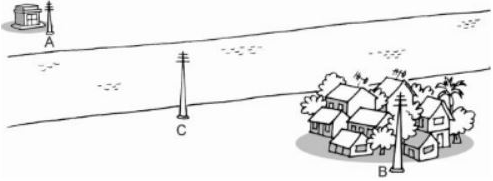
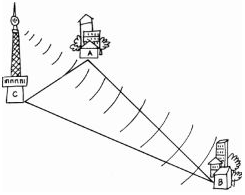
Bài 15: Một tram biến áp và một khu dân cư được xây dựng cách xa hai bờ sông tại địa điểm A và B.

Hãy tìm trên bờ sông gần khu dân cư một địa điểm C để xây dựng một cột mắc dây đưa điện từ trạm biến áp về cho khu dân cư sao cho độ dài đường dây dẫn là gần nhất.

Phương pháp giải:

+ Dựa vào định lí: Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.

+ Với ba điểm A, B, C bất kì luôn có: AB + BC ≥ AC.

Lời giải:

Để độ dài đường dây là ngắn nhất thì C nằm trên đoạn thẳng AB, tức là:

AC + BC = AB.

Thật vậy, nếu C nằm ngoài đoạn thẳng AB thì ba điểm A, B, C tạo thành một tam giác ABC. Theo định lý tổng hai cạnh trong tam giác ta có:

AC + BC > AB

Do đó AC + BC ngắn nhất khi C nằm giữa A và B.

Vậy vị trí đặt một cột mắc dây điện từ trạm về cho khu dân cư sao cho độ dài đường dây dẫn ngắn nhất là C nằm giữa A và B.

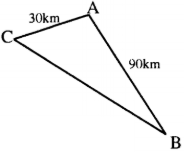
Bài 16: Ba thành phố A, B, C là ba đỉnh của một tam giác; biết rằng AC = 30km, AB = 90km (hình dưới)

a) Nếu đặt ở C máy phát sóng truyền thanh có bán kính hoạt động bằng 60km thì thành phố B có nhận được tín hiệu không? Vì sao?

b) Cũng câu hỏi như vậy với máy phát sóng có bán kính hoạt động bằng 120 km.

Phương pháp giải:

Áp dụng hệ quả của bất đẳng thức: Trong một tam giác, một cạnh bất kì luôn lớn hơn hiệu độ dài hai cạnh còn lại và lớn hơn tổng độ dài hai cạnh còn lại.

Lời giải:

Theo đề bài AC = 30km, AB = 90km ⇒ AC < AB.

Trong ∆ABC có: CB > AB – AC (hệ quả bất đẳng thức tam giác)

⇒ CB > 90 – 30 = 60km

Nếu đặt tại C máy phát sóng truyền thanh có bán kính hoạt động bằng 60km thì thành phố B không nhận được tín hiệu.

b) Trong tam giác ABC có: BC < AC + AB (bất đẳng thức tam giác).

nên BC < 30 + 90 =120km

Nếu đặt tại C máy phát sóng truyền thanh có bán kính hoạt động bằng 120km thì thành phố B nhận được tín hiệu.