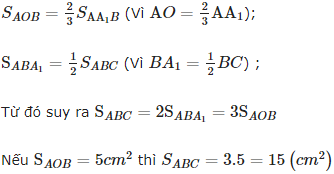Tính chất ba đường trung tuyến của tam giác (Phần 2)

TÍNH CHẤT CỦA BA ĐƯỜNG TRUNG TUYẾN (PHẦN 2)

II/ Bài tập vận dụng

2. Bài tập tự luận

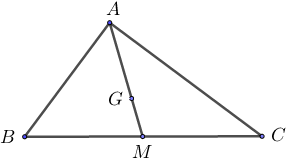
Bài 1: Tam giác ABC có trung tuyến \(AM = 9cm\) và trọng tâm G. Tính độ dài đoạn thẳng AG ?

Phương pháp giải:

Sử dụng tính chất trọng tâm tam giác.

Lời giải:

Vì G là trọng tâm tam giác ABC và AM là đường trung tuyến nên:

\(AG = \frac{2}{3}AM\) (tính chất ba đường trung tuyến của tam giác)

Do đó: \(AG = \frac{2}{3}.9 = 6cm.\)

Vậy \(AG = 6cm.\)

Bài 2: Biết rằng: Trong một tam giác vuông, đường trung tuyến ứng với cạnh bằng một nửa cạnh huyền, hãy giải bài toán sau:

Cho tam giác vuông ABC có hai cạnh góc vuông AB = 3cm, AC = 4cm. Tính cách từ đỉnh A tới trọng tâm G của tam giác ABC.

Phương pháp giải:

+ Áp dụng tính chất ba đường trung tuyến của tam giác

+ Áp dụng nhận xét: Trong một tam giác vuông, đường trung tuyến ứng với cạnh bằng một nửa cạnh huyền, hãy giải bài toán sau:

Lời giải:

Gọi M là trung điểm của BC

Suy ra: AM là trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên \(AM = \frac{1}{2}BC\)

\(\begin{array}{l}BC = \sqrt {A{B^2} + A{C^2}}  = \sqrt {{3^2} + {4^2}}  = 5cm\\ \Rightarrow AM = \frac{1}{2}.5 = 2,5cm\end{array}\)

Vì G là trọng tâm của tam giác ABC nên \(AG = \frac{2}{3}AM = \frac{2}{3}.2,5 = 1,7cm.\)

Vậy \(AG = 1,7cm.\)

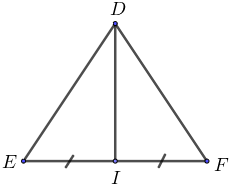
Bài 3: Cho tam giác DEF cân tại D với đường trung tuyến DI

a) Chứng minh ∆DEI  = ∆DFI

b) Các góc DIE và góc DIF là những góc gì?

c) Biết DE = DF = 13cm, EF = 10cm, hãy tính độ dài đường trung tuyến DI.

Phương pháp giải:

Áp dụng tính chất của tam giác cân, tính chất đường trung tuyến và định lý Pytago.

Lời giải:

a) ∆DEI  = ∆DFI có:

DI là cạnh chung

DE = DF ( ∆DEF cân)

IE = IF (DI là trung tuyến)

\( \Rightarrow \)  ∆DEI  = ∆DFI (c.c.c)

b) Vì \(\Delta DEI = \Delta DFI \Rightarrow \angle DIE = \angle DIF\)

Mà \(\angle BID + \angle DIF = {180^0}\) (kề bù)

Nên \(\angle DIE = \angle DIF = {90^0}\)

c) I là trung điểm của  EF nên IE = IF = 5cm

∆DEI  vuông tại I \( \Rightarrow D{I^2} = D{E^2} - E{I^2}\) (định lí pytago)

\(\begin{array}{l} \Rightarrow D{I^2} = {13^2} - {5^2} = 144\\ \Rightarrow DI = \sqrt {144}  = 12cm.\end{array}\)

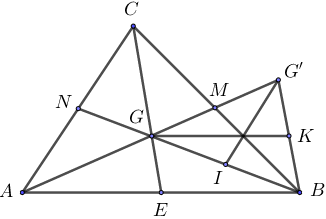
Bài 4: Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G’ sao cho G là trung điểm của AG’.

a) So sánh các cạnh của  tam giác BGG’ với các đường trung tuyến của tam giác ABC

b) So sánh các đường trung tuyến của tam giác BGG’ với các cạnh của tam giác ABC.

Phương pháp giải:

Áp dụng tính chất đường trung tuyến của tam giác.

Lời giải:

a) So sánh các cạnh của  ∆BGG’ với các đường trung tuyến của  ∆ABC BG cắt AC tại N

CG cắt AB tại E

G là trọng tâm của  ∆ABC

\( \Rightarrow GA = \frac{2}{3}AM\)

Mà GA = GG’ (G là trung điểm của AG’)

.\( \Rightarrow GG' = \frac{2}{3}AM\).

Vì G là trọng tâm của  ∆ABC \( \Rightarrow GB = \frac{2}{3}BN\)

Mặt khác: \(GM = \frac{1}{2}AG\) (G là trọng tâm)

\(AG = GG' \Rightarrow GM = \frac{1}{2}GG'\)

M là trung điểm của GG’

Do đó \(\Delta GMC = \Delta G'MB\) vì:

\(\begin{array}{l}GM = MG'\\MB = MC\\\angle GMC = \angle G'MB\\ \Rightarrow BG' = CG\end{array}\)

Mà \(CG = \frac{2}{3}CE\) (G là trọng tâm tam giác ABC)

\( \Rightarrow BG' = \frac{2}{3}CE\)

Vậy mỗi cạnh của ∆BGG' bằng \(\frac{2}{3}\)

b)  So sánh các đường trung tuyến của ∆BGG' với cạnh ∆ABC

Ta có: BM là đường trung tuyến ∆BGG'

Mà M là trung điểm của BC nên \(BM = \frac{1}{2}BC\)

Vì \(IG = \frac{1}{2}BG\) (I là trung điểm BG)

\(GN = \frac{1}{2}BG\) (G là trọng tâm)

\( \Rightarrow IG = GN\)

Do đó \(\Delta IGG' = \Delta NGA\,\,\left( {c.g.c} \right)\)

\( \Rightarrow IG' = AN \Rightarrow IG' = \frac{1}{2}AC\)

Gọi K là trung điểm BG \( \Rightarrow \) GK là trung tuyến ∆BGG'

Vì \(GE = \frac{1}{2}GC\) (G là trọng tâm ∆ABC)

\( \Rightarrow GE = \frac{1}{2}BG\)

Mà K là trung điểm BG' \( \Rightarrow \) KG' = EG

Vì ∆GMC = ∆G'BM (chứng minh trên)

\( \Rightarrow \angle GCM = \angle G'BM\) (lại góc sole trong)

\( \Rightarrow CE//BG' \Rightarrow \angle AGE = \angle AG'B\) (đồng vị)

Do đó \(\Delta AGE = \Delta GG'K\,\,\,\left( {c.g.c} \right) \Rightarrow AE = GK\)

Mà \(AE = \frac{1}{2}AB\) nên \(GK = \frac{1}{2}AB\)

Vậy mỗi đường trung tuyến ∆BGG' bằng một nửa cạnh của tam giác ABC song song với nó.

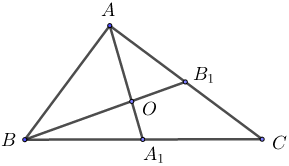
Bài 5: Trong tam giác ABC, hai đường trung tuyến \(A{A_1}\) và \(B{B_1}\) cắt nhau tại điểm O. Hãy tính diện tích tam giác ABC nếu diện tích tam giác ABO  bằng \(5c{m^2}.\)

Phương pháp giải:

Áp dụng tính chất trọng tâm và ba đường trung tuyến của tam giác.

Lời giải:

Ta có:

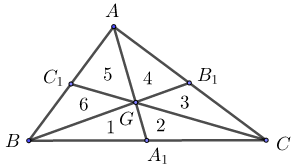
Bài 6: Chứng minh rằng các trung tuyến của một tam giác phân chia tam giác đó thành 6 tam giác mà diện tích của chúng (đôi một) bằng nhau.

Phương pháp giải:

Áp dụng tính chất trọng tâm và ba đường trung tuyến của tam giác.

Lời giải:

Xét sáu tam giác được đánh số là: 1, 2, 3, 4, 5, 6

Chứng minh hoàn toàn tương tự như bài 5 ta có:

\({S_{\Delta GAB}} = {S_{\Delta GBC}} = {S_{\Delta GCA}} = \frac{1}{3}{S_{\Delta ABC}}\)

Ta lại có: \({S_1} = {S_2}\,\,;\,\,{S_3} = {S_4}\,\,;\,\,{S_5} = {S_6}\) (vì mỗi cặp tam giác có chung đường cao và hai đáy bằng nhau)

Vậy sáu tam giác 1, 2, 3, 4, 5, 6 có diện tích bằng nhau.

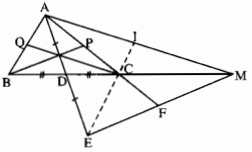
Bài 7: Cho tam giác ABC với đường trung tuyến AD. Trên tia AD lấy điểm E sao cho AD = DE, trên tia BC lấy điểm M sao cho BC = CM.

a) Tìm trọng tâm của tam giác AEM.

b) So sánh các cạnh của tam giác ABC với các đường trung tuyến của tam giác AEM

c) So sánh các đường trung tuyến của tam giác ABC với các cạnh của tam giác AEM.

Phương pháp giải:

Áp dụng tính chất ba đường trung tuyến của tam giác.

Lời giải:

a) Do AD  =  DE nên MD là một đường trung tuyến của tam giác AEM.

Hơn nữa do \(CD = \frac{1}{2}CB = \frac{1}{2}CM\)

Nên C là trọng tâm của tam giác AEM.

b) Các đường thẳng AC, EC lần lượt cắt EM, AM tại F, I.

Tam giác AEM có các đường trung tuyến là AF, EI, MD.

Ta có ∆ADB = ∆EDG (c.g.c) nên AB = EC

Vậy \(AC = \frac{2}{3}AF\,\,;\,\,BC = CM = \frac{2}{3}MD\,\,;\,\,AB = EC = \frac{2}{3}EI.\)

c) Trước tiên, theo giả thiết, ta có AD = DE nên \(AD = \frac{1}{2}AE\)

Gọi BP, CQ là các trung tuyến của ∆ABC.

\(\Delta BCP = \Delta MCF \Rightarrow BP = FM = \frac{1}{2}EM.\)

Ta sẽ chứng minh: \(CQ = \frac{1}{2}AM\)

Ta có:

\(\begin{array}{l}\Delta ABD = \Delta ECD \Rightarrow \angle BAD = \angle CED\\ \Rightarrow AB//EC \Rightarrow \angle QAC = \angle ICA\end{array}\)

Hai tam giác ACQ và CAI có cạnh AC chung, \(\angle QAC = \angle ICA,\,\,AQ = \frac{1}{2}AB = \frac{1}{2}EC = IC\)

Nên chúng bằng nhau

Suy ra CQ = AI, do đó \(CQ = \frac{1}{2}AM.\)

Vậy \(AD = \frac{1}{2}AE\,\,;\,\,BP = \frac{1}{2}EM\,\,;\,\,CQ = \frac{1}{2}AM.\)