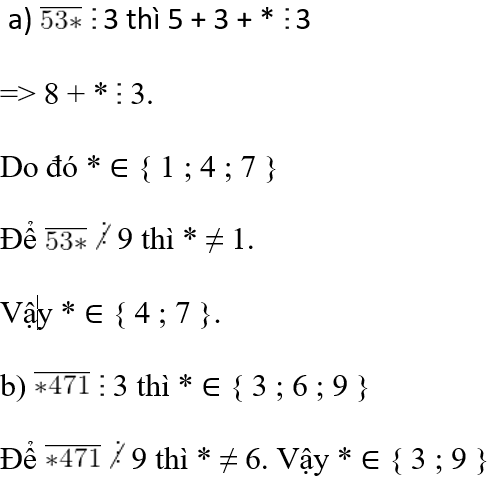Luyện tập dấu hiệu chia hết cho 3, cho 9
Cập nhật lúc: 15:04 25-10-2018 Mục tin: LỚP 6
Bài viết bao gồm các bài tập bổ trợ kèm lời giải để các em luyện tập về dấu hiệu chia hết cho 3,9
Xem thêm:
LUYỆN TẬP
DẤU HIỆU CHIA HẾT CHO 3, CHO 9
Câu 1: Trong các số: \(5319;{\rm{ }}3240;{\rm{ }}831\):
- Số nào chia hết cho 3 mà không chia hết cho 9?
- Số nào chia hết cho cả 2, 3, 5, 9?
Lời giải:
a, - Số 5319
- có tổng các chữ số: 5 + 3 + 1 + 9 = 18
- \(18 \vdots 3,{\rm{ }}18 \vdots 9\)
nên 5319 chia hết cho 3 và cho 9
- Số 3240
- có tổng các chữ số: 3 + 2 + 4 + 0 = 9
- \(9 \vdots 3,{\rm{ }}9 \vdots 9\)
nên 3240 chia hết cho 3 và cho 9
- Số 831
- có tổng các chữ số: 8 + 3 + 1 = 12
- \(12 \vdots 3,{\rm{ }}12\;\not \vdots 9\)
nên số 831 chia hết 3 mà không chia hết cho 9.
b, Số chia hết cho 2 và cho 5 có chữ số tận cùng là 0
Kết hợp với kết quả câu a nên số chia hết cho 2, 3, 5, 9 là 3240.
Câu 2: Điền chữ số vào dấu * để:
- 3*5 chia hết cho 3
- 7*2 chia hết cho 9
- *63* chia hết chi cả 2, 3, 5, 9.
Lời giải:
\(\begin{array}{l}a)\;\;\overline {3*5} \;{\rm{ }} \vdots {\rm{ }}3\\ = > {\rm{ }}3{\rm{ }} + {\rm{ }}*{\rm{ }} + {\rm{ }}5\; \vdots \;3{\rm{ }} = > {\rm{ }}8{\rm{ }} + {\rm{ }}*\; \vdots \;3\\ = > {\rm{ }}*\; \in \left\{ {{\rm{ }}1{\rm{ }};{\rm{ }}4{\rm{ }};{\rm{ }}7{\rm{ }}} \right\}\\b)\;\;\overline {7*2} \;{\rm{ }} \vdots {\rm{ }}9\\ = > {\rm{ }}7{\rm{ }} + {\rm{ }}*{\rm{ }} + {\rm{ }}2\; \vdots \;9{\rm{ }} = > {\rm{ }}9{\rm{ }} + {\rm{ }}*\; \vdots \;9 = > {\rm{ }}\\*\; \in \;{\rm{ }}\left\{ {{\rm{ }}0{\rm{ }};{\rm{ }}9{\rm{ }}} \right\}\\c)\;\;\overline {a63b} \; \vdots \;5\\ = > {\rm{ }}b{\rm{ }} = {\rm{ }}0\\\overline {a630} \; \vdots \;3,\; \vdots \;9\\ = > {\rm{ }}a{\rm{ }} + {\rm{ }}6{\rm{ }} + {\rm{ }}3{\rm{ }} + {\rm{ }}0\; \vdots \;9\\ = > {\rm{ }}9{\rm{ }} + {\rm{ }}a\; \vdots \;9{\rm{ }} = > {\rm{ }}a{\rm{ }} = {\rm{ }}9\end{array}\)
Câu 3: Viết số tự nhiên nhỏ nhất có bốn chữ số sao cho số đó:
- Chia hết cho 3
- Chia hết cho 9
Lời giải:
a. Số tự nhiên nhỏ nhất có bốn chữ số chia hết cho 3 có dạng \(\overline {100a} \)
Ta có: \(\overline {100a} \vdots 3 \Leftrightarrow \left( {1{\rm{ }} + {\rm{ }}0{\rm{ }} + {\rm{ }}0{\rm{ }} + {\rm{ }}a} \right) \vdots 3 \Leftrightarrow \left( {1{\rm{ }} + {\rm{ }}a} \right) \vdots 3\)
Suy ra: \(a \in \left\{ {2;{\rm{ }}5;{\rm{ }}8} \right\}\)
Vậy số tự nhiên nhỏ nhất có bốn chữ số chia hết cho 3 là 1002.
b. Số tự nhiên nhỏ nhất có bốn chữ số chia hết cho 9 có dạng \(\overline {100a} \)
Ta có: \(100a \vdots 9 \Leftrightarrow \left( {1{\rm{ }} + {\rm{ }}0{\rm{ }} + {\rm{ }}0{\rm{ }} + {\rm{ }}a} \right) \vdots 9 \Leftrightarrow \left( {1{\rm{ }} + {\rm{ }}a} \right) \vdots 9\)
Suy ra: \(a \in \left\{ 8 \right\}\)
Vậy số tự nhiên nhỏ nhất có bốn chữ số chia hết cho 9 là 1008.
Câu 4: Tổng (hiệu) sau có chia hết cho 3, cho 9 không?
\(\begin{array}{l}1.\;\;\;\;\;\;\;\;\;\;\;\;\;{10^{12}}-{\rm{ }}1\\2.\;\;\;\;\;\;\;\;\;\;\;\;\;{10^{10\;}} + {\rm{ }}2\end{array}\)
Lời giải:
a. Số \({10^{12\;}}\) có tổng các chữ số là 1 + 0 + 0 + … + 0 = 1
* Vì 1 chia cho 3 dư 1 nên 1012 chia cho 3 dư 1.
⇒ \({10^{12\;}}\) – 1 chia hết cho 3.
* Vì 1 chia 9 dư 1 nên 1012 chia cho 9 dư 1.
⇒ \({10^{12\;}}\) – 1 chia hết cho 9.
b. Số \({10^{10}}\)có tổng các chữ số là 1 + 0 + 0 + … + 0 = 1
⇒ \({10^{10}}\) + 2 có tổng các chữ số là 1 + 0 + 0 + … + 0 + 2 = 3
Vì 3 chia hết cho 3 nhưng không chia hết cho 9.
Vậy 1010 + 2 chia hết cho 3 nhưng không chia hết cho 9.
Câu 5: Điền chữ số vào dấu * để được số chia hết cho 3 mà không chia hết cho 9?
a. 53* b. *471
Lời giải:
Câu 6: Tìm chữ số a và b sao cho a – b = 4 và \(87ab \vdots 9\)
Lời giải:
Ta có: \(87ab \vdots 9 \Leftrightarrow \left( {8{\rm{ }} + {\rm{ }}7{\rm{ }} + {\rm{ }}a{\rm{ }} + {\rm{ }}b} \right) \vdots 9 \Leftrightarrow \left( {15{\rm{ }} + {\rm{ }}a{\rm{ }} + {\rm{ }}b} \right){\rm{ }} \vdots {\rm{ }}9\)
Suy ra: \(\left( {a{\rm{ }} + {\rm{ }}b} \right) \in \left\{ {3;{\rm{ }}12} \right\}\)
Vì a – b = 4 nên a + b > 3. Suy ra a + b = 12
Thay a = 4 + b vào a + b = 12, ta có:
\(\begin{array}{*{20}{l}}{b{\rm{ }} + {\rm{ }}\left( {4{\rm{ }} + {\rm{ }}b} \right){\rm{ }} = {\rm{ }}12 \Leftrightarrow 2b{\rm{ }} = {\rm{ }}12{\rm{ }}-{\rm{ }}4}\\{ \Leftrightarrow 2b{\rm{ }} = {\rm{ }}8 \Leftrightarrow b{\rm{ }} = {\rm{ }}4}\\{a{\rm{ }} = {\rm{ }}4{\rm{ }} + {\rm{ }}b{\rm{ }} = {\rm{ }}4{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}8}\end{array}\)
Vậy ta có số: 8784.
Bài tập bổ sung
Bài 1: Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
a) Nếu a + b + c = 9 thì ;
b) Nếu a + b + c = 18 thì ;
c) Nếu thì a + b + c = 9.
Bài 2*: Có bao nhiêu số tự nhiên có ba chữ số và chia hết cho 3?
Bài 3*: Cho \(n = \overline {7a5} + \overline {8b4} \). Biết a – b = 6 và n chia hết cho 9. Tìm a và b.
Giải
Bài 1:
a) Đúng ;
b) Sai ;
c) Sai
Bài 2*:
Các số tự nhiên có ba chữ số và chia hết cho 3 là 102, 105, 108,…, 999, gồm
(999 – 102) : 3 + 1 = 300 (số).
Bài 3*:
Ta biết rằng một số và tổng các chữ số của nó có cùng số dư khi chia cho 9.
Tổng \(n = \overline {7a5} + \overline {8b4} \) chia hết cho 9 nên \(7{\rm{ }} + {\rm{ }}a{\rm{ }} + {\rm{ }}5{\rm{ }} + {\rm{ }}8{\rm{ }} + {\rm{ }}b{\rm{ }} + {\rm{ }}4\; \vdots \;9\), tức là \(24{\rm{ }} + {\rm{ }}a{\rm{ }} + {\rm{ }}b\; \vdots \;9\). Suy ra \(a{\rm{ }} + {\rm{ }}b\; \in \left\{ {{\rm{ }}3{\rm{ }};{\rm{ }}12{\rm{ }}} \right\}.\)
Ta có a + b > 3 (vì a – b = 6) nên a + b = 12.
Từ a + b = 12 và a – b = 6, ta có \(a{\rm{ }} = {\rm{ }}\left( {12{\rm{ }} + {\rm{ }}6} \right){\rm{ }}:{\rm{ }}2{\rm{ }} = {\rm{ }}9\), suy ra b = 3.
Thử lại : 795 + 834 = 1629, chia hết cho 9.
Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:
>> Học trực tuyến lớp 6 chương trình mới trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 6 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
- Ôn tập chương II - Góc(10/12)
- Luyện tập về tam giác (Có đáp án)(10/12)
- Luyện tập về Đường tròn (Có lời giải)(10/12)
- Luyện tập tia phân giác của góc (Có lời giải)(10/12)
- Vẽ góc cho biết số đo (Có đáp án)(10/12)
- Khi nào thì góc xOy + góc yOx = góc xOz? (Có đáp án)(10/12)
- Luyện tập về số đo góc (Có đáp án)(10/12)
- Luyện tập về góc (Có đáp án)(10/12)
- Luyện tập về nửa mặt phẳng - Có đáp án(10/12)
- Luyện tập tính chất cơ bản của phép nhân phân số(21/11)
chuyên đề được quan tâm
- Chương 1: Khảo sát và vẽ đồ thị hàm số
- Chương 2: Hình học không gian
- Chương 3: Hàm số mũ - hàm số logarit
- Chương 4: Nguyên hàm - tích phân
- Toàn bộ công thức toán học
- Căn bậc hai, Căn bậc ba
- Tổng hợp các đề kiểm tra 1 tiết chương 1...
- Chương 1: Mệnh đề - Tập hợp
- Chương 1: Hàm số lượng giác và phương trình lượng...
- Chương 2: Tổ hợp - xác suất - nhị thức...
bài viết mới nhất
- Các bất đẳng thức THCS cơ bản và nâng cao
- Tính chất ba đường trung tuyến của tam giác (Phần...
- Tính chất ba đường trung tuyến của tam giác (Phần...
- Quan hệ giữa ba cạnh của một tam giác. Bất...
- Quan hệ giữa ba cạnh của một tam giác. Bất...
- Quan hệ giữa ba cạnh của một tam giác. Bất...
- Quan hệ giữa đường vuông góc và đường xiên, đường...
- Quan hệ giữa góc và cạnh đối diện trong một...
- Ôn tập chương 8: Thống kê (Phần 2)
- Ôn tập chương 8: Thống kê (Phần 1)
Cập nhật thông tin mới nhất của kỳ thi tốt nghiệp THPT 2025