LUYỆN TẬP DỰNG HÌNH

LUYỆN TẬP DỰNG HÌNH

A. Lý thuyết

1. Bài toán dựng hình

Ta đã biết vẽ hình bằng nhiều dụng cụ: thước, compa, êke…. Ta xét các bài toán vẽ hình mà chỉ sử dụng hai dụng cụ là thước và compa, chúng được gọi là các bài toán dựng hình.

Với thước, ta có thể:

Câu 1: Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 5cm, B = 35^o

Lời giải:

Cách dựng:

- Dựng đoạn BC = 5cm

- Dựng góc ∠CBx = 35^o

- Dựng CA ⊥ Bx ta có ΔABC dựng được.

Chứng minh: ΔABC có ∠A = 90^o, ∠B = 35^o, BC = 5cm. Thỏa mãn điều kiện bài toán.

Câu 2: Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 4,5cm và cạnh góc vuông AC = 2cm

Lời giải:

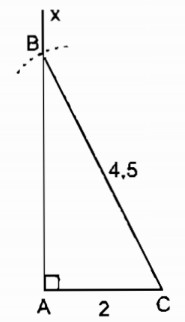
Cách dựng:

- Dựng đoạn AC = 2cm.

- Dựng góc ∠(CAx) bằng 90^o.

- Dựng cung tròn tâm C bán kinh 4,5cm cắt AX tại B. Nối CB ta có ΔABC cẩn dựng .

Chứng minh:

ΔABC có ∠A = 90^o, AC = 2 cm, BC = 4,5 cm.

Thỏa mãn điều kiện bài toán.

Câu 3: Dựng hình thang cân ABCD (AB // CD), biết CD = 3cm, AC = 4cm, ∠D = 70^o

Lời giải:

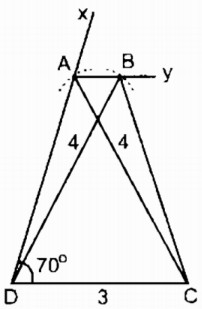
Phân tích: Giả sử hình thang ABCD dựng được thỏa điểu kiện bài toán, ta thấy ΔACD xác định được vì biết CD = 3cm, ∠D = 70^o, AC = 4cm

Ta cẩn xác định đỉnh B. Đỉnh B thỏa mãn 2 điểu kiện:

- Nằm trên tia Ay//CD

- B cách D một khoảng bằng 4cm.

Cách dụng:

- Dựng đoạn CD = 3cm

- Dựng góc CDx bằng 70^o

- Trên nửa mặt phẳng bờ CD chứa tia Dx dựng cung tròn tâm C bản kính 4cm cắt Dx tại A.

- Dựng tia Ay // CD

- Trên nữa mặt phẳng bờ CD chứa điểm A, dựng cung tròn tâm D bán kính 4cm cắt Ay tại B

- Nối BC ta có hình thang ABCD cần dựng.

Chứng minh: Thật vậy theo cách dựng, ta có AB // CD nên tứ giác ABCD là hình thang có CD = 3cm , ∠D = 70^o, AC = 4cm.

Vậy ABCD là hình thang cân.

Biện luận: ΔACD luôn dựng được nên hình than ABCD luôn dựng được.

Bài toán có một nghiệm hình.

Câu 4: Dựng hình thang ABCD (AB //CD) biết AD = 2cm, ∠D = 90^o, DC = 4cm.

Lời giải:

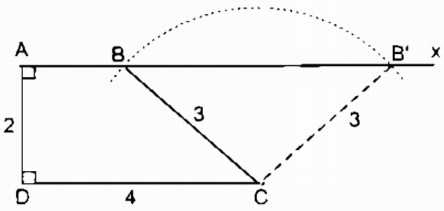
Phân tích: Giả sử hình thang ABCD dựng được thỏa mãn bài toán.

Ta thấy ΔADC xác định được vì biết AD = 2cm, ∠D = 90^o, DC = 4cm. Ta cần xác định đình B. Đỉnh B thỏa mãn hai điều kiện:

- B nằm trên tia Ax//CD

- B cách C một khoảng bằng 3cm

Cách dựng:

- Dựng ΔADC biết:

AD = 2cm, D = 90^o, DC = 4cm

- Dựng Ax ⊥ AD

- Dựng cung tròn tâm C bản kính bằng 3cm, cắt Ax tại B.

Nối BC ta có hình thang ABCD dựng được.

Chứng minh:

Thật vậy theo cách dựng, ta có: AB // CD, ∠D = 90^o

Tứ giác ABCD là hình thang vuông

Lại có AD = 2cm, CD = 4cm, BC = 3cm

Hình thang dựng được thỏa mãn điều kiện bài toán.

Biện luận: Δ ADC dựng được, hình thang ABCD luôn dựng được.

Bài toán có hai nghiệm hình.

Câu 5: Dựng ΔABC cân tại A, biết BC = 3cm, đường cao BH = 2,5cm.

Lời giải:

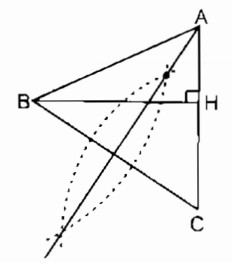
Cách dựng:

- Dựng BH : 2,5cm

- Dựng ∠(xHB) = 90^o

- Dựng cung tròn tâm B bán kính 3cm cắt Hx tại C.

- Dựng BC

- Dựng đường trung trực BC cắt CH tại A

- Dựng AB, ta có ΔABC cẩn dựng

Chứng minh:

Ta có AC = AB (tính chất đường trung trực)

Nên ΔABC cân tại A, BH ⊥ AC

Ta lại có BC = 3cm, BH = 2,5cm

Vậy ΔABC dựng được thỏa mãn điều kiện bài toán.

Câu 6: Dựng tam giác ABC, biết BC = 4cm , ∠B = 40^o , AC = 3cm

Lời giải:

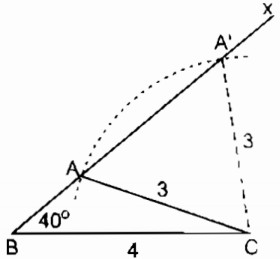
Cách dựng:

- Dựng đoạn thẳng BC = 4cm .

- Dựng góc ∠(CBx) bằng 40^o

- Dựng trên nửa mặtphẳng bờ BC chứa tia Bx cung tròn tâm C bản kính 3cm cắt BX tại A.

- Kẻ AC, ta có tam giác ABC cần dựng.

Chứng minh:

Thật vậy, theo cách dựng Δ ABC có BC = 4cm, ∠B = 40^o, AC = 3cm.

Thỏa mãn điều kiện bài toán

Bài toán có hai nghiệm hình.

Câu 7: Dựng hình thang ABCD (AB // CD) biết AD = 2cm, DC = 4cm, AC = 3,5cm, BC = 2,5cm

Lời giải:

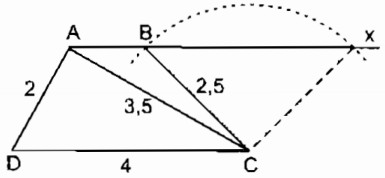
Phân tích: Giả sử hình thang ABCD dựng được thỏa mãn điều kiện bài toán.

Tam giác ADC dựng được vì biết ba cạnh AD = 2cm, DC = 4cm, AC = 3,5cm. Điểm B thỏa mãn hai điều kiện:

- B nằm trên đường thẳng đi qua A và song song với CD.

- B cách C một khoảng bằng 2,5cm.

Cách dựng:

- Dựng ΔADC biết AD = 2cm, DC = 4cm, AC = 3,5cm

- Dựng tia Ax // CD. Ax nằm trong nửa mặt phẳng bờ AD chứa điểm G.

- Dựng cung tròn tâm C bán kính 2,5cm. Cung này cắt Ax tại B, nối CB ta có hình thang ABCD cần dựng.

Chứng minh:

Tứ giác ABCD là hình thang vì AB // CD.

Hình thang ABCD có: AD = 2cm, CD = 4cm, AC = 3,5cm, BC = 2,5cm thỏa mãn yêu cầu bài toán.

Biện luận: Vì ΔADC luôn dựng được nên hình thang ABCD dựng được 2 hình thang thỏa mãn bài toán.

Câu 8: Dựng hình thang cân ABCD có AB // CD, biết AD = 2cm, CD = 4cm, AC = 3,5cm

Lời giải:

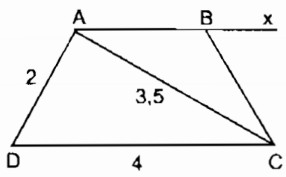
Phân tích: Giả sử hình thang ABCD dựng được thỏa mãn điều kiện bài toán. Tam giác ADC dựng được vì biết ba cạnh AD = 2cm, CD = 4cm, AC= 3,5cm. Điểm B thỏa mãn 2 điều kiện:

- B nằm trên đường thẳng đi qua A và song song với CD.

- B cách D một khoảng bằng 3,5cm.

Cách dựng:

- Dựng ΔADC biết:

AD = 2cm, AC = 3,5cm, CD = 4cm.

- Dựng tia AX // CD. Ax nằm trong nửa mặt phẳng bờ AD chứa điểm C.

- Dựng cung tròn tâm D bán kính 3,5cm. Cung này cắt AX tại B. Nối CB, ta có hình thang ABCD cần dựng.

Chứng minh:

Tứ giác ABCD là hình thang vì AB //CD.

AC = BD = 3,5cm

Vậy hình thang ABCD là hình thang cân.

Hình thang cân ABCD có: AD = 2cm, CD = 4cm, AC = 3,5cm thỏa mãn yêu cầu bài toán.

Biện luận: Tam giác ADC luôn dựng được nên hình thang ABCD luôn dựng được. Cung tròn tâm D bán kính 3,5cm cắt Ax tại 1 điểm nên ta dựng được một hình thang thỏa mãn yêu cầu bài toán.

Câu 9: Dựng hình thang cân ABCD có AB//CD, biết hai đáy AB = 2cm, CD = 4cm, đường cao AH = 2cm.

Lời giải:

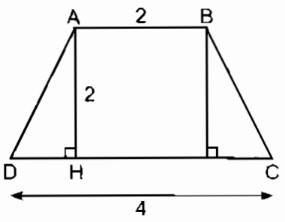
Phân tích: Giả sử hình thang ABCD dựng được thỏa mãn điều kiện bài toán. Tam giác ADH dựng được vì biết hai cạnh góc vuông AH = 2cm và HD = lcm, ∠H = 90o và đáy AB < CD nên ∠D < 90^o. Điểm H nằm giữa D và C.

Điểm C nằm trên tia đối tia HD và cách H

Điểm B thỏa mãn hai điều kiện:

- B nằm trên đường thẳng đi qua A và song song với DH.

- B cách A một khoảng bằng 2cm

Cách dựng:

- Dựng ΔAHD biết ∠H = 90^o, AH = 2cm, HD = lcm

- Dựng tia đối tia HD

- Dựng điểm C sao cho HC = 3cm

- Dựng tia AX // DH, Ax nằm trên nửa mặt phẳng bờ AD chứa điểm H.

- Dựng điểm B sao cho AB = 2cm . Nối CB ta có hình thang ABCD cẩn dựng.

Chứng minh:

Tứ giác ABCD là hình thang vì AB//CD.

Kẻ BK ⊥ CD. Tứ giác ABKH là hình thang có 2 cạnh bên song song nên: BK = AH và KH = AB

Suy ra: KC = HC - KH = HC - AB = 3 - 2 = 1 (cm)

Suy ra: ΔAHD = ΔBKC (c.g.c) ⇒ ∠D = ∠C

Câu 10: Dựng hình thang ABCD, biết hai đáy AB = 2cm, CD = 4cm, ∠D = 70^o, ∠C = 50^o

Lời giải:

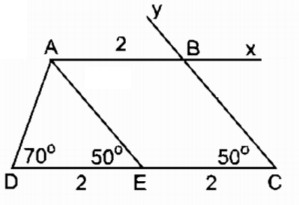
Phân tích:

Giả sử hình thang ABCD dựng được thỏa mãn điều kiện bài toán. Qua A kẻ đường thẳng song song với BC cắt CD tại E. Hình thang ABCE có 2 cạnh bên song song nên AB = EC = 2cm do đó DE = 2cm

Tam giác ADE dựng được vì biết 2 góc kề với một cạnh.

Điểm C nằm trên tia DE cách D một khoảng bằng 4cm.

Điểm B thỏa mãn hai điều kiện:

- B nằm trên đường thẳng đi qua A và song song với CD.

- B nằm trên đường thẳng đi qua C và song song với AE.

Cách dựng:

- Dựng ΔADE biết DE = 2cm, ∠D = 70^o, E = 50^o

- Dựng tia DE lấy điểm C sao cho DC = 4cm

- Dựng tia AX // CD, Ax nằm trên nửa mặt phẳng bờ AD chứa điểm C

- Dựng tia Cy // AE, Cy nằm trên nửa mặt phẳng bờ CD chưa điểm A.

Cy cắt Ax tại B. Hình thang ABCD cần dựng.

Chứng minh:

Tứ giác ABCD là hình thang vì AB // CD.

CD = CE + ED ⇒ CE = CD – ED = 4 – 2 = 2 (cm)

Hình thang ABCE có hai cạnh bên AE // CB

⇒ AB = CE = 2 (cm)

∠C = ∠E = 50^o (hai góc đồng vị)

∠D = 70o

Hình thang ABCD thỏa mãn điều kiện bài toán.

Biện luận: Tam giác ADE luôn dựng được, hình thang ABCD luôn dựng được. Ta dựng được một hình thang thỏa mãn điều kiện bài toán.

Vậy hình thang ABCD là hình thang cân.

Hình thang cân ABCD có: AH = 2cm, đáy AB = 2cm, đáy CD = 4cm thỏa mãn điều kiện bài toán.

Biện luận: Tam giác AHD luôn dựng được nên hình thang ABCD luôn dựng được. Ta luôn được một hình thang thỏa mãn điều kiện bài toán.