LUYỆN TẬP ĐỐI XỨNG TÂM
Cập nhật lúc: 12:57 14-11-2018 Mục tin: LỚP 8
Bài viết sẽ cung cấp cho em các kiến thức liên quan đến đối xứng tâm. Thông qua phần lý thuyết được trình bày chi tiết ở phần A, các em có thể áp dụng để giải các bài tập liên quan ở phần B. Sau khi làm xong, các em hay đối chiếu với đáp án bên dưới để so sánh kết quả nhé.
Xem thêm:
LUYỆN TẬP ĐỐI XỨNG TÂM
A. Lý thuyết
1. Hai điểm đối xứng qua một điểm
Hai điểm gọi đối xứng với nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.
![]()
A và A’ đối xứng nhau qua O ⇔{A,O,A′thẳnghàngOA′=OA">⇔A,O,A′ thẳnghàng và OA′=OA
2. Hai hình đối xứng qua một điểm
Hai hình gọi là đối xứng với nhau qua điểm O nếu mỗi điểm của hình này đối xứng với một điểm thuộc hình kia qua điểm O và ngược lại.
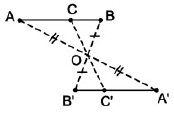
Tính chất:
Nếu hai đoạn thẳng AB và A’B’ có các điểm A và A’, B và B’ đối xứng với nhau qua điểm O thì:
– AB = A’B’
– AB và A’B’ đối xứng với nhau qua O.
Chú ý: Trong đối xứng tâm:
– Hình đối xứng với một đường thẳng là một đường thẳng song song với nó.
– Hình đối xứng của một góc là một góc bằng nó.
– Hình đối xứng của một tam giác là một tam giác bằng nó.
– Hình đối xứng của một đường tròn là một đường tròn bằng nó.
3. Hình có tâm đối xứng
Điểm O gọi là tâm đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua điểm O cũng thuộc hình H.
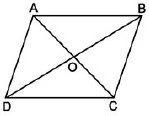
Một vài hình có tâm đối xứng quen thuộc:
– Đường tròn có tâm đối xứng là tâm của nó
– Hình bình hành có tâm đối xứng là giao điểm của hai đường chéo.
Định lí:
Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó.
B. Bài tập
Câu 1: Cho hình vẽ, trong đó ABCD là hình bình hành. Chứng minh rằng điểm M đối xứng với điểm N qua điểm C.
Lời giải:
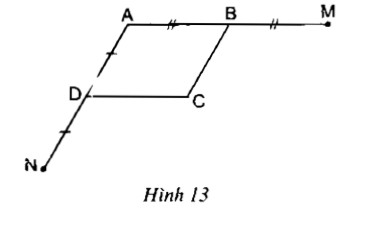
Tứ giác ABCD là hình bình hành:
⇒ AB // CD hay BM // CD
Xét tứ giác BMCD ta có:
BM // CD
BM = CD (gt)
Suy ra: Tứ giác BMCD là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ MC // BD và MC = BD (1)
AD // BC (gt) haỵ DN // BC
Xét tứ giác BCND ta có: DN // BC và DN = BC (vì cùng bằng AD)
Suy ra: Tứ giác BCND là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ CN // BD và CN = BD (2)
Từ (1) và (2) suy ra: M, C, N thẳng hàng và MC = CN.
Câu 2: Cho hình vẽ trong đó DE // AB, DF // AC.Chứng minh rằng điểm E đối xứng với điểm F qua điểm I.
Lời giải:
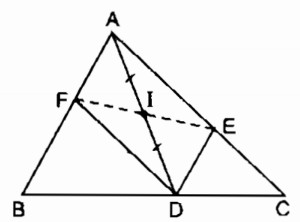
Ta có: DE //AB (gt) hay DE //AF
DF //AC (gt) hay DF //AE
Tứ giác AEDF là hình bình hành.
I là trung điểm của AD nên EF đi qua trung điểm I là IE = IP (tính chất hình bình hành)
Vậy E và F đối xứng qua tâm I.
Câu 3: Cho tam giác ABC, các đường trung tuyến BM, CN. Gọi D là điểm đối xứng với B qua M, gọi E là điểm đối xứng Với C qua N. Chứng minh rằng điểm D đối xứng với điểm E qua điểm A.
Lời giải:
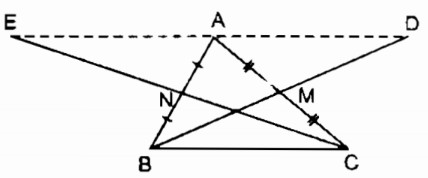
* Xét tứ giác ABCD, ta có:
MA = MC (gt)
MB = MD (định nghĩa đối xứng tâm)
Suy ra: Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
⇒ AD // BC hay AD = BC (1)
* Xét tứ giác ACBE, ta có:
AN = NB (gt)
NC = NE (định nghĩa đối xứng tâm)
Suy ra: Tứ giác ACBE là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường) ⇒ AE // BC và AE = BC (2)
Từ (1) và (2) suy ra: A, D, E thẳng hàng và AD = AE
Nên A là trung điểm của DE hay điểm D đối xứng với điểm E qua điểm A.
Câu 4: Cho tam giác ABC vuông tại A, điểm D thuộc cạnh BC. Gọi E là điểm đối xứng với D qua AB, gọi F là điểm đối xứng với D qua AC. Chứng minh rằng các điểm E và F đối xứng với nhau qua điểm A.
Lời giải:
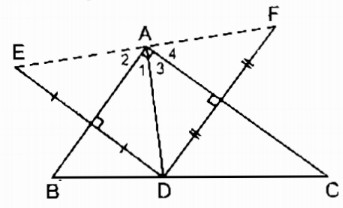
* Vì E đối xứng với D qua AB
⇒ AB là đường trung trực của đoạn thẳng DE
⇒ AD = AE (tỉnh chất đường trung trực)
Nên ΔADE cân tại A
Suy ra: AB là đường phân giác của ∠(DAE) ⇒ ∠A1= ∠A2
* Vì F đối xứng với D qua AC
⇒ AC là đường trung trực của đoạn thẳng DF
⇒ AD = AF (tính chất đường trung trực)
Nên ΔADF cân tại A
Suy ra: AC là phân giác của ∠(DAF)
⇒ ∠A3= ∠A4
∠(EAF) = ∠(EAD) + ∠(DAF) = ∠A1+ ∠A2+ ∠A3+ ∠A4= 2(∠A1+ ∠A3) = 2.90o= 180o
⇒ E, A, F thẳng hàng có AE = AF = AD
Nên A là trung điểm của EF hay điểm E đối xứng với điểm F qua điểm A.
Câu 5: Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh đối AD, BC ở E, F. Chứng minh E và F đối xứng với nhau qua điểm O.
Lời giải:
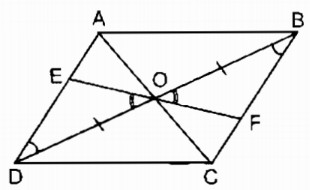
Xét ΔOED và ΔOFB, ta có:
∠(EOD)= ∠(FOB)(đối đỉnh)
OD = OB (tính chất hình bình hành)
∠(ODE)= ∠(OBF)(so le trong)
Do đó: ΔOED = ΔOFB (g.c.g)
⇒ OE = OF
Vậy O là trung điểm của EF hay điểm E đối xứng với điểm F qua điểm O
Câu 6: Cho hình bên, trong đó ABCD là hình bình hành. Chứng minh H và K đối xứng với nhau qua điểm O
Lời giải:
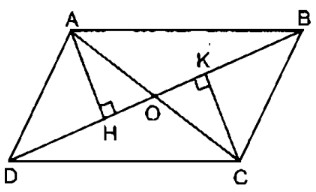
Xét hại tam giác vuông AHO và CKO, ta có:
∠(AHO)= ∠(CKO)= 90o
OA = OC (tính chất hình bình hành)
∠(AOH)= ∠(COK)(đối đỉnh)
Suy ra: ΔAHO = ΔCKO (cạnh huyền, góc nhọn)
⇒ OH = OK
Vậy O là trung điểm của HK hay điểm H đối xứng với điểm K qua điểm O
Câu 7: Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Gọi O là một điểm bất kỳ nằm trong tam giác ABC. Vẽ điểm M đối xứng với O qua D. Vẽ điểm N đối xứng với O qua E. Chứng minh rằng MNCB là hình bình hành.
Lời giải:
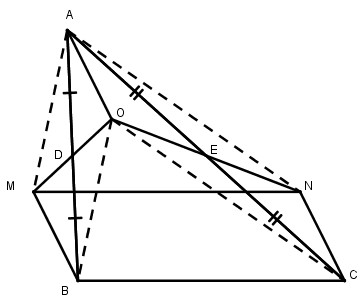
* Xét tứ giác AOBM, ta có:
DA = DB (gt)
DO = DM (định nghĩa đối xứng tâm)
Suy ra: Tứ giác AOBM là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
⇒ BM // AO và BM = AO (1)
* Xét tứ giác AOCN, ta có: EA = EC (gt)
EO = EN (định nghĩa đối xứng tâm)
Suy ra: Tứ giác AOBM là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
⇒ CN // AO và CN = AO (2)
Từ (1) và (2) suy ra:BM // CN và BM = CN.
Vậy tứ giác BMNC là hình bình hành (vì có 1 cặp cạnh đối song song và bằng nhau).
Câu 8: Cho tam giácABC, các đường trungtuyến AD, BE, CF cắt nhau tại G. Gọi H là điểm đối xứng với G qua D, I là điểm đối xứng với G qua E, K là điểm đối xứng với G qua F. Tìm các điểm đối xứng với A, với B, với C qua G.
Lời giải:
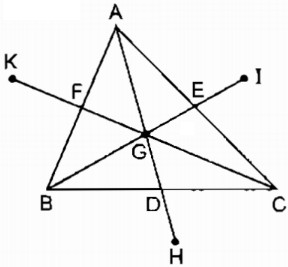
* Ta có: GD = DH (tính chất đối xứng tâm)
⇒ GH = 2GD (l)
GA = 2GD (tính chất đường trung tuyến của tam giác) (2)
Từ (1) và (2) suy ra: GA = GH
Suy ra điểm đối xứng với điểm A qua tâm G là H.
* Ta có: GE = EI (tính chất đối xứng tâm)
⇒ GI = 2GB (3)
GB = 2GE (tính chất đường trung tuyên của tam giác) (4)
Từ (3) và (4) suy ra: GB = GI
Suy ra điểm đối xứng với điểm B qua tâm G là I.
GF = FK (tỉnh chất đối xứng tâm)
⇒ GK = 2GF (5)
GC = 2GF (tính chất đường trung tuyến của tam giác) (6)
Từ (5) và (6) Suy ra: GC = GK
Suy ra điểm đối xứng với điểm C qua tâm G là điểm K
Câu 9: Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Qua O kẻ đường thẳng cắt đường thẳng cắt hai cạnh AB, CD ở E, F. Qua O vẽ đường thẳng cắt hai cạnh AD, BC ở G, H. Chứng minh rằng EGFH là hình bình hành.
Lời giải:
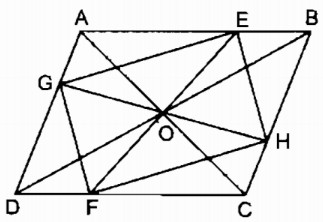
* Xét ΔOAE và ΔOCF, ta có:
OA = OC (tính chất hình bình hành)
∠(AOE)= ∠(COF)(đối đỉnh)
∠(OAE)= ∠(OCF)(so le trong)
Do đó: ΔOAE = ΔOCF (g.c.g)
⇒ OE = OF (l)
* Xét ΔOAG và ΔOCH, ta có:
OA = OC (tính chất hình bình hành)
∠(AOG) = ∠(COH)(dối đỉnh)
∠(OAG) = ∠(OCH)(so le trong).
Do đó: ΔOAG = ΔOCH (g.c.g)
⇒ OG = OH (2)
Từ (1) và (2) suy ra tứ giác EGFH là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường).
Câu 10: Cho góc xOy, điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm G đối xứng với A qua Oy.
a, Chứng minh rằng OB = OC
b, Tính số đo góc xOy để B đối xứng với C qua O
Lời giải:
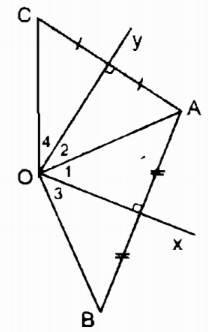
a, Vì B đối xứng với A qua trục Ox nên Ox là đường trung trực của đoạn AB.
⇒ OA = OB (tính chất đường trung trực) (1)
Vì C đối xứng với A qua trục Ọy nên Oy là đườngtrung trực của đoạn AC.
⇒ OA = OC (tỉnh chất đường trung trực) (2)
Từ (l) và (2) suy ra: OB = OC.
b, Vì OB = OC nên để điểm B đối xứng với C qua tâm O cần thêm điều kiện B, O, C thằng hàng
ΔOAB cân tại O có Ox là đường trung trực của AB nên Ox cũng là đường phân giác của ∠(AOB) ⇒ ∠O1= ∠O3
ΔOAC cân tại O có Oy là đường trung trực của AC nên Oy cũng là đường phân giác của ∠(AOC) ⇒ ∠O2= ∠O4
Vì B, O, C thẳng hàng nên:
∠O1+∠O2+∠O3+∠O4 = 180o ⇒ 2 ∠O1+ 2 ∠O2= 180o
⇒ ∠O1+∠O2= 90o ⇒ ∠(xOy) = 90o
Vậy ∠(xOy) = 90o thì B đối xứng với C qua tâm O
Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:
>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
- Ôn tập hình học chương 1 (THCS Yên Nghĩa 2017 -2018)(26/12)
- Ôn tập chương 6 - Diện tích đa giác (có đáp án)(18/12)
- Luyện tập Diện tích đa giác (có đáp án) (18/12)
- Luyện tập Diện tích hình thoi (có đáp án) (17/12)
- Luyện tập Diện tích hình thang (có đáp án) (17/12)
- Luyện tập Diện tích tam giác (có đáp án) (tiếp theo)(17/12)
- Luyện tập Diện tích tam giác (có đáp án)(17/12)
- Luyện tập Diện tích hình chữ nhật (có đáp án)(17/12)
- Luyện tập Đa giác - Đa giác đều (có đáp án)(17/12)
- Ôn tập chương II - Phân thức đại số (tiếp) - Có đáp án(12/12)
chuyên đề được quan tâm
- Chương 1: Khảo sát và vẽ đồ thị hàm số
- Chương 2: Hình học không gian
- Chương 3: Hàm số mũ - hàm số logarit
- Chương 4: Nguyên hàm - tích phân
- Toàn bộ công thức toán học
- Căn bậc hai, Căn bậc ba
- Tổng hợp các đề kiểm tra 1 tiết chương 1...
- Chương 1: Mệnh đề - Tập hợp
- Chương 1: Hàm số lượng giác và phương trình lượng...
- Chương 2: Tổ hợp - xác suất - nhị thức...
bài viết mới nhất
- Các bất đẳng thức THCS cơ bản và nâng cao
- Tính chất ba đường trung tuyến của tam giác (Phần...
- Tính chất ba đường trung tuyến của tam giác (Phần...
- Quan hệ giữa ba cạnh của một tam giác. Bất...
- Quan hệ giữa ba cạnh của một tam giác. Bất...
- Quan hệ giữa ba cạnh của một tam giác. Bất...
- Quan hệ giữa đường vuông góc và đường xiên, đường...
- Quan hệ giữa góc và cạnh đối diện trong một...
- Ôn tập chương 8: Thống kê (Phần 2)
- Ôn tập chương 8: Thống kê (Phần 1)
Cập nhật thông tin mới nhất của kỳ thi tốt nghiệp THPT 2025


