|
Lý Thuyết
1. Định lí. Với số a không âm và số b dương ta có
\( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\).
Lưu ý. a) Với biểu thức A ≥ 0 và B > 0 thì không thể viết đẳng thức trên. Chẳng hạn \( \frac{\sqrt{-9}}{\sqrt{-4}}\) được xác định nhưng biểu thức \( \frac{\sqrt{-9}}{\sqrt{-4}}\) không xác định.
2. Quy tắc khai phương một thương
Muốn khai phương một thương \( \frac{a}{b}\), trong đó a không âm, b dương, ta có thể khai phương lần lượt a và b rồi lấy kết quả thứ nhất chia cho kết quả thứ 2.
3. Quy tắc chia các căn bậc hai
Muốn chia các căn bậc hai của số a không âm cho căn bậc hai của số b dương ta có thể chia a cho cho b rồi khai phương kết quả đó.
Bài Tập
Bài 28 trang 18 sgk toán 9 - tập 1
Bài 28. Tính:
a) \( \sqrt{\frac{289}{225}}\) b) \( \sqrt{2\frac{14}{25}}\)
c) \( \sqrt{\frac{0,25}{9}}\) d) \( \sqrt{\frac{8,1}{1,6}}\)
Hướng dẫn giải
ĐS: a) \( \frac{17}{15}\); b) \( \frac{8}{5}\);
c) \( \frac{1}{6}\) ; d) \( \frac{9}{4}\).
Bài 29 - 34 trang 19 sgk toán 9 - tập 1
Bài 29. Tính
a) \( \frac{\sqrt{2}}{\sqrt{14}}\);
b) \( \frac{\sqrt{15}}{\sqrt{735}}\);
c) \( \frac{\sqrt{12500}}{\sqrt{500}}\);
d) \( \frac{\sqrt{6^{5}}}{\sqrt{2^{3}.3^{5}}}\).
Hướng dẫn giải: Áp dụng quy tắc chia hai căn thức bậc hai.
ĐS: a) \( \frac{1}{3}\); b) \( \frac{1}{7}\); c) 5; d) 2.
Bài 30. Rút gọn các biểu thức sau:
a) \( \frac{x}{y}.\sqrt{\frac{x^{2}}{y^{4}}}\) với x > 0, y ≠ 0; b) 2\( y^{2}\).\( \sqrt{\frac{x^{4}}{4y^{2}}}\) với y < 0;
c) 5xy.\( \sqrt{\frac{25x^{2}}{y^{6}}}\) với x < 0, y > 0; d) 0,2\( x^{3}y^{3}.\sqrt{\frac{16}{x^{4}y^{8}}}\) với x ≠ 0, y ≠ 0.
Hướng dẫn giải:
a) \( \frac{y}{x}.\sqrt{\frac{x^{2}}{y^{4}}}\) = \( \frac{y}{x}\).\( \frac{\sqrt{x^{2}}}{\sqrt{y^{4}}}\) = \( \frac{y}{x}\).\( \frac{\left | x \right |}{y^{2}}\) = \( \frac{x}{xy}\) vì x > 0.
Do đó \( \frac{y}{x}.\sqrt{\frac{x^{2}}{y^{4}}}\) = \( \frac{1}{y}\).
b) \( 2y^{2}.\sqrt{\frac{x^{4}}{4y^{2}}}\) = \( 2y^{2}\).\( \frac{\sqrt{x^{4}}}{\sqrt{4y^{2}}}\) = \( 2y^{2}\).\( \frac{x^{2}}{2\left | y \right |}\).
Vì y < 0 nên │y│= -y. Do đó \( 2y^{2}.\sqrt{\frac{x^{4}}{4y^{2}}}\) = \( 2y^{2}\).\( \frac{x^{2}}{-2y}\) = \( -x^{2}y\).
c) 5xy.\( \sqrt{\frac{25x^{2}}{y6}}\) = 5xy.\( \frac{\sqrt{25x^{2}}}{\sqrt{y^{6}}}\) = 5xy.\( \frac{5\left | x \right |}{\left | y^{3} \right |}\).
Vì x < 0, y > 0 nên \( \left | x \right |\) = -x và \( \left | y^{3} \right |\) = \( y^{3}\).
Do đó: 5xy\( \sqrt{\frac{25x^{2}}{y6}}\) = 5xy.\( \frac{-5x}{y^{3}}\) = -\( \frac{25x^{2}}{y^{2}}\).
d) 0,2\( x^{3}y^{3}.\sqrt{\frac{16}{x^{6}y^{8}}}\) = \( 0,2x^{3}y^{3}\frac{\sqrt{16}}{\sqrt{x^{6}y^{8}}}\) = 0,2\(0.2 x^{3}y^{3}\frac{4}{\left | x^{3} \right |y^{4}}\) = \( \frac{0,8x^{2}}{\left | x^{3} \right |y}\)
Nếu x > 0 thì \( x^{3}\) > 0 nên \( \left | x^{3} \right |= x^{3}\). Do đó 0,2\( x^{3}y^{3}.\sqrt{\frac{16}{x^{6}y^{8}}}\) = \( \frac{0,8}{y}\).
Nếu x < 0 thì \( x^{3}\) < 0 nên \( \left | x^{3} \right |= -x^{3}\). Do đó 0,2\( x^{3}y^{3}.\sqrt{\frac{16}{x^{6}y^{8}}}\) = -\( \frac{0,8}{y}\).
Bài 31.
a) So sánh \( \sqrt{25 - 16}\) và √25 - √16;
b) Chứng minh rằng: với a > b >0 thì √a - √b < \( \sqrt{a - b}\).
Hướng dẫn giải:
a) HD: Thực hiện phép khai căn rồi so sánh kết quả.
Trả lời: \( \sqrt{25 - 16}\) > √25 - √16;.
b) HD: Ta có thể chứng minh rằng √a < \( \sqrt{a - b}\) + √b.
Nhưng điều này suy ra từ kết quả bài tập 26.b) SGK nếu lưu ý rằng
√a = \( \sqrt{(a - b)+b}\).
Bài 32. Tính
a) \( \sqrt{1\frac{9}{16}.5\frac{4}{9}.0,01}\); b) \( \sqrt{1,44.1,21-1,44.0,4}\);
c) \( \sqrt{\frac{165^{2}-124^{2}}{164}}\); d) \( \sqrt{\frac{149^{2}-76^{2}}{457^{2}-384^{2}}}\).
Hướng dẫn giải:
a) HD: Đổi hỗn số và số thập phân thành phân số.
ĐS: \( \frac{35}{120}\).
b) \( \sqrt{1,44.1,21-1,44.0,4}\) = \( \sqrt{\frac{144}{100}.\frac{121}{100}-\frac{144}{100}.\frac{40}{100}}\)
= \( \sqrt{\frac{144}{100}\left ( \frac{121}{100} -\frac{40}{100}\right )}\) = \( \sqrt{\frac{144.81}{100.100}}\) = \( \frac{\sqrt{144.81}}{100}\)
= \( \frac{12.9}{100}=\frac{18}{100}=\frac{27}{25}\).
d) ĐS: \( \frac{15}{29}\).
Bài 33. Giải phương trình
a) √2.x - √50 = 0; b) √3.x + √3 = √12 + √27;
c) √3.\( x^{2}\) - √12 = 0; d) \( \frac{x^{2}}{\sqrt{5}}\) - √20 = 0.
Hướng dẫn giải:
a) √2.x - √50 = 0 \( \Leftrightarrow\) √2.x = √50 \( \Leftrightarrow\) x = \( \frac{\sqrt{50}}{\sqrt{2}}\)
\( \Leftrightarrow\) x = \( \sqrt{\frac{50}{2}}\) = √25 = 5.
b) ĐS: x = 4.
c) √3.\( x^{2}\) - √12 = 0 \( \Leftrightarrow\) √3.\( x^{2}\) = √12 \( \Leftrightarrow\) \( x^{2}\) = \( \frac{\sqrt{12}}{\sqrt{3}}\) \( \Leftrightarrow\) \( x^{2}\) = \( \sqrt{\frac{12}{3}}\)
\( \Leftrightarrow\) \( x^{2}\) = √4 \( \Leftrightarrow\) \( x^{2}\) = 2 \( \Leftrightarrow\) x = √2 hoặc x = -√2.
d) ĐS: x = √10 hoặc x = -√10.
Bài 34. Rút gọn các biểu thức sau:
a) \( ab^{2}.\sqrt{\frac{3}{a^{2}b^{4}}}\) với a < 0, b ≠ 0; b) \( \sqrt{\frac{27(a - 3)^{2}}{48}}\) với a > 3;
c) \( \sqrt{\frac{9+12a+4a^{2}}{b^{2}}}\) với a ≥ -1,5 và b < 0; d) (a - b).\( \sqrt{\frac{ab}{(a - b)^{2}}}\) với a < b < 0.
Hướng dẫn giải:
a) ĐS: -√3. b) ĐS: \( \frac{3}{4}\)(a - 3).
c) \( \sqrt{\frac{9+12a+4a^{2}}{b^{2}}}\) = \( \sqrt{\frac{(3+2a)^{2}}{b^{2}}}\) = \( \frac{\sqrt{(3+2a)^{2}}}{b^{2}}\) = \( \frac{\left | 3+2a \right |}{\left | b \right |}\)
Vì b < 0 nên \( \left | b \right |\) = -b.
Vì a > -1,5 nên 3 + 2a > 0. Do đó = 3+ 2a.
Vậy \( \sqrt{\frac{9+12a+4a^{2}}{b^{2}}}\) = -\( \frac{3+2a}{b}\).
d) ĐS: -\( \sqrt{ab}\)
Bài 35,36,37 trang 20 sgk toán 9 - tập 1
Bài 35. Tìm x, biết:
a) \(\sqrt{(x-3)^{2}}=9;\)
b) \(\sqrt{4x^{2}+4x+1}=6.\)
Hướng dẫn giải:
a) \(\sqrt {{{\left( {x - 3} \right)}^2}} = 9 \Leftrightarrow \left| {x - 3} \right| = 9\)
Khi \(x\geq 3\) thì \(x-3\geq 0.\) Do đó \(\left | x-3 \right |=x-3.\)
Ta phải giải phương trình \(x-3=9.\) Suy ra \(x=12\).
Vì 12>3 nên x=12 là một nghiệm.
Khi x
Ta phải giải phương trình \(-x+3=9.\) Suy ra \(x=-6.\)
Vì -6
Vậy phương trình đã cho có hai nghiệm: x=12 và x=-6.
b) HD: Đổi \(4x^{2}+4x+1\) thành bình phương của một tổng.
ĐS: \(x=\frac{5}{2}\) và \(x=-\frac{7}{2}\).
Bài 36. Mỗi khẳng định sau đúng hay sai ? Vì sao ?
a) \(0,01=\sqrt{0,0001};\)
b)\(-0,5=\sqrt{-0,25};\)
c) \(\sqrt{39}< 7\) và \(\sqrt{39}>6\);
d) \(\left( 4- \sqrt{13} \right)\cdot 2x< \sqrt{3}(4-\sqrt{13})\Leftrightarrow 2x< \sqrt{3}.\)
Hướng dẫn giải:
a) Đúng
b) Sai. Số âm không có căn bậc hai.
c) Đúng vì \(7=\sqrt{49}\) và \(6=\sqrt{36}\).
d) Đúng vì \(4=\sqrt{16}> \sqrt{13};\) do đó \(4-\sqrt{13}>0.\)
Bài 37. Đố: Trên lưới ô vuông, mỗi ô vuông cạnh 1cm, cho bốn điểm M, N, P, Q (h.3).
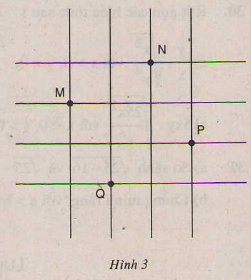
Hãy xác định số đo cạnh, đường chéo và diện tích của tứ giác MNPQ.
Hướng dẫn giải:
Tứ giác MNPQ có:
- Các cạnh bằng nhau và cùng bằng đường chéo của hình chữ nhật có chiều dài 2cm, chiều rộng 1cm. Do đó theo định lí Py-ta-go:
\(MN=NP=PQ=QM=\sqrt{2^{2}+1^{2}}=\sqrt{5} (cm)\).
- Các đường chéo bằng nhau và cùng bằng đường chéo của hình chữ nhật có chiều dài 3cm, chiều rộng 1cm nên độ dài đường chéo là:
\(MP=NQ=\sqrt{3^{2}+1^{2}}=\sqrt{10}(cm).\)
Từ các kết quả trên suy ra MNPQ là hình vuông. Vậy diện tích tứ giác MNPQ bằng \(MN^{2}=(\sqrt{5})^{2}=5(cm)\).
|








