Hình chữ nhật. Tính chất về khoảng cách giữa hai đường thẳng song song

HÌNH CHỮ NHẬT. TÍNH CHẤT VỀ KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG SONG SONG

A. KIẾN THỨC CẦN NHỚ

1. Định nghĩa

Hình chữ nhật là tứ giác có 4 góc vuông (h.29).

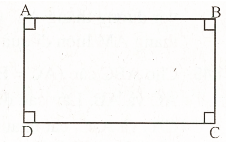
Như vậy hình chữ nhật cũng là hình bình hành, hình thang cân. 

2. Tính chất

Hình chữ nhật có tất cả các tính chất của hình bình hành, hình thang cân.

Như vậy : Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.

3. Dấu hiệu nhận biết

• Tứ giác có ba góc vuông là hình chữ nhật.
• Hình thang cân có một góc vuông là hình chữ nhật.
• Hình bình hành có một góc vuông là hình chữ nhật.
• Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

4. Áp dụng vào tam giác vuông

• Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền (h.30).

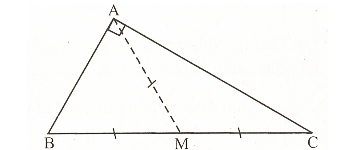
• Đảo lại, nếu một tam giác có đường trung tuyến ứng với một cạnh bằng một nửa cạnh ấy thì tam giác đó là tam giác vuông.

                   \(\Delta \)ABC ; MB = MC

                    \(\widehat {\rm{A}}{\rm{  =  90^\circ }}\) có AM = \(\frac{1}{2}\)BC.

5. Bổ sung

• Hình chữ nhật có một tâm đối xứng là giao điểm của hai đường chéo.
• Hình chữ nhật có hai trục đối xứng là hai đường thẳng đi qua trung điểm hai cạnh đối.

6. Đường thẳng song song vói đường thẳng cho trưóc

    6.1. Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm tùy ý trên đường thẳng này đến đường thẳng kia.

    6.2.  

• Tính chất: Các điểm cách đường thẳng b một khoảng bằng h nằm trên hai đường thẳng song song với b và cách b một khoảng bằng h (h.31).        

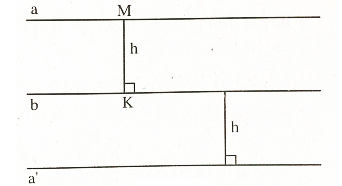
• Nhận xét : Tập hợp các điểm cách một đường thẳng cố định một khoảng bằng h không đổi là hai đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng bằng h.

    6.3. Đường thẳng song song cách đều

• Nếu các đường thẳng song song cách đều cắt một đường thẳng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau (h.32).

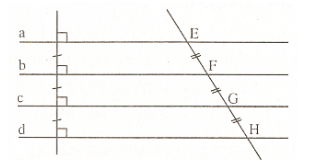
• Đảo lại, nếu các đường thẳng song song cắt một đường thẳng và chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau thì chúng song song cách đều.

    6.4. Bổ sung

Cho hai đường thẳng a và b song song với nhau và cách nhau một khoảng h. Các điểm cách đều a và b thì nằm trên đường thẳng m song song với a và b và

cách hai đường thẳng đó một khoảng \(\frac{{\rm{h}}}{{\rm{2}}}\)

B. MỘT SỐ VÍ DỤ

Ví dụ 13. Cho hình thang cân ABCD (AB//CD). Gọi O là giao điểm của hai đường chéo và M, N, P theo thứ tự là trung điểm của AO, DO, BC. Nếu \(\widehat {{\rm{AOB}}}{\rm{  =  60^\circ }}\)thì tam giác MNP là tam giác gì ?

Giải (h.33)

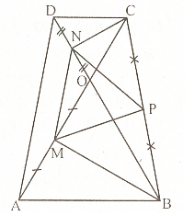
     ABCD là hình thang cân => \(\Delta \)ABD = \(\Delta \)BAC (c.c.c)

     => \(\widehat {{\rm{ABD}}}{\rm{  =  }}\widehat {{\rm{BAC}}}\); mà \(\widehat {{\rm{AOB}}}{\rm{  =  60^\circ   =  >  }}\Delta {\rm{OAB}}\) đều.

     BM là đường trung tuyến => BM là đường cao BM.

     => BM \( \bot \)AO

     \(\Delta \)BMC có\(\widehat {{\rm{BMC}}}{\rm{  =  90^\circ }}\), MP là đường trung tuyến

     => MP = \(\frac{1}{2}\)BC.

     Tương tự ta có NP = \(\frac{1}{2}\)BC. 

     Mặt khác MN là đường trung bình của \(\Delta \)OAD => MN = \(\frac{1}{2}\)AD. Mà AD = BC

    => MP = NP = MN=>\(\Delta \)MNP đều.

Ví dụ 14. Cho hình chữ nhật ABCD. Gọi H là hình chiếu của B trên AC. Gọi I và N là trung điểm của AD và HC. Chứng minh rằng BN\( \bot \)IN.

Giải (h.34)

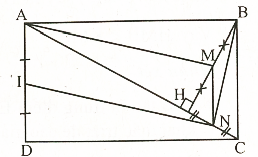
     Gọi M là trung điểm của BH

     => MN // BC, MN = \(\frac{1}{2}\)BC

     Do đó AINM là hình bình hành

     => AM // IN .                                                        (1)

     Mặt khác \(\Delta \)ABN có BH là đường cao, MN là đường cao (vì MN // BC,

BC\( \bot \)AB) nên M là trực tâm => AM\( \bot \)BN                    (2)

     Từ (1) và (2) suy ra BN\( \bot \)IN.

    Nhận xét. Với kỹ thuật trên, có thể giải được bài toán hay và khó hơn sau : Cho hình chữ nhật ABCD. Gọi H là hình chiếu của B trên AC. Gọi E, F, M lần lượt là trung điểm AB, DH, BH. Chứng minh rằng AM\( \bot \)EF.

Ví dụ 15. Cho tam giác ABC (AB < AC) và P là điểm nằm trong tam giác sao cho

\(\widehat {{\rm{PBA}}}{\rm{  =  }}\widehat {{\rm{PCA}}}\). Gọi H và K lần lượt là chân các đường vuông góc hạ từ P xuống AB và AC ; M là trung điểm của BC. Chứng minh rằng :                                

a) MH = MK ;      

b) \(\widehat {{\rm{HMB}}}{\rm{  <  }}\widehat {{\rm{KMC}}}{\rm{.}}\)

Giải (h.35)

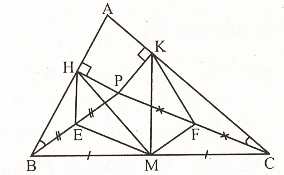
a) Gọi E, F theo thứ tự là trung điểm của PB và PC.

Suy ra \(\widehat {{\rm{HEP}}}{\rm{  =  2}}{\rm{.}}\widehat {{\rm{PBH}}}{\rm{ ; }}\widehat {{\rm{KFP}}}{\rm{  =  2}}{\rm{.}}\widehat {{\rm{KCP}}}{\rm{  =  >  }}\widehat {{\rm{HEP}}}{\rm{  =  }}\widehat {{\rm{KFP}}}\).   (1)

Mặt khác, dễ có PEMF là hình bình hành =>\(\widehat {{\rm{PEM}}}{\rm{  =  }}\widehat {{\rm{PFM}}}{\rm{ }}{\rm{.}}\)      (2)

Từ (1) và (2) ta có : \(\widehat {{\rm{HEM}}}{\rm{  =  }}\widehat {{\rm{KFM}}}\)

Sử dụng tính chất đường trung tuyến trong tam giác vuông và đường trung bình của tam giác, ta.có : EM = KF (=\(\frac{1}{2}\)PC); HE = MF (=\(\frac{1}{2}\)BP).

Do đó : \(\Delta \)HEM = \(\Delta \)MFK (c.g.c) => MH = MK.

b) \(\Delta \)HEM = \(\Delta \)MFK => \(\widehat {{\rm{HME}}}{\rm{  =  }}\widehat {{\rm{MKF}}}\)                       (3)

Vì AB < AC => \(\widehat {{\rm{ABC}}}{\rm{  >  }}\widehat {{\rm{ACB}}}{\rm{  >  }}\widehat {{\rm{PCB}}}{\rm{ }}\left( {{\rm{v\`i  }}\widehat {{\rm{PBH}}}{\rm{  =  }}\widehat {{\rm{PCK}}}} \right){\rm{.}}\)

Suy ra\(\widehat {{\rm{FMC}}}{\rm{  >  }}\widehat {{\rm{FCM}}}{\rm{  =  >  MF  <  FC v\`a  }}\widehat {{\rm{FMC}}}{\rm{  >  }}\widehat {{\rm{EMB}}}\) (4)

Từ MF < FC => MF < FK =>\(\widehat {{\rm{KMF}}}{\rm{  >  }}\widehat {{\rm{MKF}}}\)            (5)

Từ (3), (4) và (5) suy ra \(\widehat {{\rm{HME}}}{\rm{  +  }}\widehat {{\rm{EMB}}}{\rm{  <  }}\widehat {{\rm{KMF}}}{\rm{  +  }}\widehat {{\rm{FMC}}}\).

Vậy \(\widehat {{\rm{HMB}}}{\rm{  <  }}\widehat {{\rm{KMC}}}{\rm{.}}\)

Nhận xét

• Việc tạo ra trung điểm E, F đã tạo ra mối liên kết giữa giả thiết với nhau và khai thác triệt để các giả thiết ấy.
• Với kỹ thuật trên, có thể giải được bài toán sau : Cho tam giác ABC, về phía ngoài tam giác vẽ \(\widehat {{\rm{BAx}}}{\rm{  =  }}\widehat {{\rm{CAy}}}{\rm{  =  21^\circ }}{\rm{.}}\)Hạ BE vuông góc với Ax, CF vuông góc với Ay. Gọi M là trung điểm của BC. Chứng minh tam giác MEF cân và tính các góc của tam giác ấy.

(Tuyển sinh lớp 10, THPT chuyên ĐHKHTN Hà Nội, năm học 1989 - 1990).

C. BÀI TẬP

1. Cho hình chữ nhật ABCD có tâm O, điểm M nằm trên đoạn OB, điểm E đối xứng với A qua M, điểm H là chân đường vuông góc kẻ từ E tới BC. Vẽ hình chữ nhật EHCF. Chứng minh rằng M, H, F thẳng hàng.

2. Cho \(\Delta \)ABC vuông tại A (AC > AB), đường cao AH. Trên tia HC lấy điểm D sao cho HD = HA. Đường vuông góc với BC tại D cắt AC tại E.

a) Chứng minh AE = AB.

b) Gọi M là trung điểm của BE. Tính số đo\(\widehat {{\rm{AHM}}}\).

3. Cho tam giác ABC vuông tại A có AM là đường trung tuyến. Gọi D là một điểm thuộc AM. Kẻ DI vuông góc với AB, DK vuông góc với AC.

a) Chứng minh rằng IK // BC.

b) Xác định vị trí điểm D trên AM sao cho IK = \(\frac{1}{3}\)BC.

4. Cho \(\Delta \)ABC vuông tại A có AH, AM tương ứng là đường cao, đường trung tuyến. Kẻ HD, HE lần lượt vuông góc với AB, AC. Kẻ MK vuông góc với AB. Gọi N là giao điểm của AM và HE. Chứng minh rằng :

a) AM\( \bot \)DE ;

b) BN // DE ;

c) MK, BN, AH đồng quy.

5. Cho hình chữ nhật ABCD (AB > BC). Lấy điểm E trên cạnh AD. Lấy F, K

trên cạnh CD sao cho DF = CK < \(\frac{1}{2}\)CD. Vẽ đường thẳng vuông góc với EK

tại K cắt BC tại M. Chứng minh rằng \(\Delta \)MEF vuông.

6. Cho \(\Delta \)ABC nhọn có BD ; CE là đường cao. Gọi I, K là hình chiếu của B và C trên đường thẳng DE. Chứng minh rằng DK = EI.

7. Cho hình chữ nhật ABCD, điểm E thuộc cạnh AB. Trên tia đối của tia CB lấy điểm I sao cho \(\widehat {{\rm{EDI}}}{\rm{  =  90^\circ }}{\rm{.}}\)Vẽ hình chữ nhật EDIK. Chứng minh rằng \(\widehat {{\rm{DBK}}}{\rm{  =  90^\circ }}{\rm{.}}\)

8. Cho \(\Delta \)ABC cân tại A. Lấy điểm D thuộc cạnh BC. Kẻ Dx vuông góc với BC, cắt AB, AC tại E và F. Vẽ hình chữ nhật BDEH và DCKF. Gọi I và O là tâm của hình chữ nhật BDEH, DCKF.

a) Chứng minh rằng AIDO là hình t)ình hành.

b) Chứng minh A là trung điểm của HK.

c) Gọi M là trung điểm của OI. Khi D di động trên BC, chứng minh rằng M nằm trên đoạn thẳng \({\rm{I}}_{\rm{1}}^{}{\rm{O}}_{\rm{1}}^{}\), trong đó \({\rm{I}}_{\rm{1}}^{}{{\rm{,}}^{}}{\rm{O}}_{\rm{1}}^{}\)lần lượt là trung điểm của AB, AC.

9. Cho tứ giác ABCD có độ dài các cạnh là AB = \(\sqrt 3 \), BC = 3, CD = \(2\sqrt 3 \), DA = \(3\sqrt 3 \) và \(\widehat {\rm{A}}{\rm{  =  6}}{{\rm{0}}^{\rm{0}}}\). Tính các góc còn lại của tứ giác ABCD.

10. Đố. Bạn Toán và bạn Học chơi một trò chơi sau : Bạn Toán xếp một đồng tiền xu lên mặt bàn hình chữ nhật. Sau đó, bạn Học lại xếp một đồng tiền xu lên mặt bàn, cứ tiếp tục như vậy, hai bạn thay       nhau  xếp... sao cho không có hai đồng xu nào chồng lên nhau. Bạn nào xếp được đồng xu cuối cùng lên mặt bàn thì bạn đó thắng cuộc. Bạn Toán đi trước, hỏi có cách nào để luôn thắng cuộc hay không ? Bạn hãy chỉ giúp.