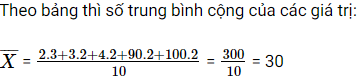Số trung bình cộng
Cập nhật lúc: 12:45 22-02-2019 Mục tin: LỚP 7
Bài viết này sẽ giúp các em biết được khái niệm, ý nghĩa và công thức tính số trung bình cộng từ bảng số liệu thống kê hoặc bảng tần số; biết được thế nào là mốt của dấu hiệu và áp dụng vào làm các bài tập trắc nghiệm và tự luận.
SỐ TRUNG BÌNH CỘNG
I/ Tóm tắt lý thuyết
1. Số trung bình cộng
a) Khái niệm
Số trung bình cộng của một dấu hiệu X, kí hiệu \(\overline X \) là số dùng làm đại diện cho một dấu hiệu khi phân tích hoặc so sánh nó với các biến lượng cùng loại.
b) Quy tắc tìm số trung bình cộng
Số trung bình cộng của một dấu hiệu được tính từ bảng tần số theo cách sau:
- Nhân từng giá trị với tần số tương ứng
- Cộng tất cả các tích vừa tìm được
- Chia tổng đó cho các giá trị (tức tổng các tần số)
Ta có công thức: \(\overline X = \frac{{{x_1}{n_1} + {x_2}{n_2} + {x_3}{n_3} + ... + {x_k}{n_k}}}{N}\)
Trong đó:
c) Ý nghĩa của số trung bình cộng
- Ý nghĩa: Số trung bình cộng thường được dùng làm "đại diện" cho dấu hiệu, đặc biệt là khi muốn so sánh các dấu hiệu cùng loại.
- Chú ý:
+ Khi các giá trị của dấu hiệu có khảng cách chênh lệch rất lớn đối với nhau thì không nên lấy số trung bình cộng là “đại diện” cho dấu hiệu đó.
Ví dụ: Xét dấu hiệu X có dãy giá trị là: \(4000\,\,\,\,\,\,\,\,\,\,1000\,\,\,\,\,\,\,\,\,500\,\,\,\,\,\,\,\,\,100.\)
Không thể lấy số trung bình cộng \(\overline X = 1400\) là đại diện cho X vì có sự chênh lệch rất lớn giữa các giá trị (chẳng hạn \(4000\) và \(100\)).
+ Số trung bình cộng có thể không thuộc dãy giá trị của dấu hiệu.
2. Mốt của dấu hiệu
Mốt của dấu hiệu là giá trị có tần số lớn nhất trong bảng tần số. Kí hiệu là \({M_0}.\)
3. Ví dụ minh họa
Ví dụ 1: Xạ thủ A và B thi bắn súng, mỗi người bắn 10 phát súng, kêt quả điểm như sau:
Tính điểm trung bình của mỗi xạ thủ và cho biết ai bắn tốt hơn.
Phương pháp:
Lời giải chi tiết:
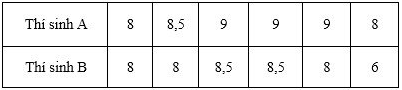
Ví dụ 2: Điểm của Ban giám khảo cho các thí sinh A và B như sau:
Tính điểm trung bình của mỗi thí sinh và cho biết ai được bước tiếp vào vòng trong.
Lời giải chi tiết:
Ví dụ 3: Trung bình cộng của tám số là 12. Do thêm số thứ chín nên trung bình cộng của chín số là 13. Tìm số thứ chín.
Lời giải chi tiết:
Tổng của tám số lúc đầu là: 12.8=96.
Tổng của chín số là: 13.9=117.
Số thứ chín là: 117-96=21.
Vậy số thứ chín là 21.
Ví dụ 4: Một bảng thống kê cho biết tỉ số giữa số nữ và số nam là 11:10. Tuổi thọ trung bình của nữ là 34, tuổi thọ trung bình của nam là 32. Tính tuổi trung bình của những người được thống kê.
Lời giải chi tiết:
Dạng 1: Câu hỏi trắc nghiệm:
Chọn đáp án trước câu trả lời đúng:
Câu 1: Phát biểu nào sau đây là sai:
A. Số trung bình cộng thường được dùng để làm đại diện cho dấu hiệu, đặc biệt là khi so sánh các dấu hiệu cùng loại.
B. Số trung bình cộng luôn thuộc dãy giá trị của dấu hiệu.
C. Mốt của dấu hiệu là giá trị có tần số lớn nhất trong bảng “tần số”
D. Khi các giá trị của dấu hiệu có khoảng chênh lệch rất lớn đối với nhau thì không nên lấy số trung bình cộng làm “đại diện” cho dấu hiệu đó.
Câu 2: Trung bình cộng của sáu số là 4. Do thêm số thứ bảy nên trung bình cộng của bảy số là 5. Số thứ bảy là:
A. 11 B. 12 C. 13 D. 14
Câu 3: Trung bình cộng của các giá trị thay đổi như thế nào nếu mỗi giá trị tăng a đơn vị:
A. Giảm a đơn vị B. Giảm 2a đơn vị
C. Tăng 2a đơn vị D. Tăng a đơn vị
Câu 4: Điểm trung bình 10 bộ môn của An như sau:
6,2 6,3 7,2 7,5 7,5 8,4 8,6 8,8 8,8 9,0
Điểm trung bình của An là:
A. 7,1 B. 7,08 C. 7,2 D. 7,09
Câu 5: Một học sinh viết 27 số rồi tính trung bình cộng của chúng, nhưng sau đó học sinh này lại viết tiếp số trung bình cộng đó bên cạnh rồi tính luôn số trung bình cộng của 28 số. Số trung bình cộng lúc sau lớn hơn, nhỏ hơn hay bằng số trung bình cộng lúc đầu?
A. Lớn hơn B. Nhỏ hơn
C. Bằng D. Không thể biết được
Đáp án: 1B, 2A, 3D, 4B, 5C
Dạng 2: Bài tập tự luận
Bài 1:
Lời giải chi tiết:
Bài 2: Quan sát bảng “tần số” (bảng 24) và cho biết có nên dùng số trung bình cộng làm “đại diện” cho dấu hiệu không? Vì sao?
Lời giải chi tiết:
Số trung bình cộng này chênh lệch quá lớn so với các giá trị trong bảng. Do đó trong trường hợp này không nên dùng số trung bình cộng làm “đại diện” cho dấu hiệu.
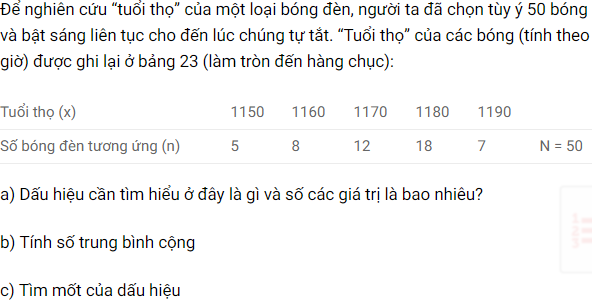
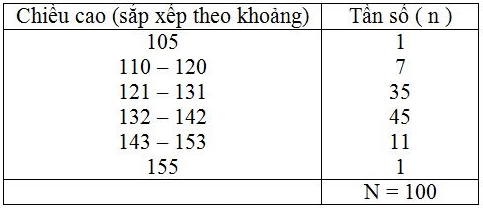
Bài 3: Đo chiều cao của 100 học sinh lớp 6 (đơn vị đo: cm) và được kết quả theo bảng sau:
a) Bảng này có gì khác so với những bảng “tần số” đã biết?
b) Ước tính số trung bình cộng trong trường hợp này.
Phương pháp:
- Kẻ thêm vào sau cột chiều cao là cột số trung bình cộng của từng lớp; sau cột tần số là cột tích giữa trung bình cộng.
- Nhân từng giá trị của trung bình cộng mỗi lớpvới tần số tương ứng
- Cộng tất cả các tích vừa tìm được
- Chia tổng đó cho các giá trị (tức tổng các tần số) để tìm số trung bình cộng.
Lời giải chi tiết:
a) Bảng này có khác so với bảng tần số đã học.
Các giá trị khác nhau của biến lượng được "phân lớp" trong các lớp đều nhau (10 đơn vị) mà không tính riêng từng giá trị khác nhau.
b) Số trung bình cộng
Để tiện việc tính toán ta kẻ thêm vào sau cột chiều cao là cột số trung bình cộng của từng lớp; sau cột tần số là cột tích giữa trung bình cộng.
Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:
>> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
- Lý thuyết về số hữu tỉ(07/09)
- So sánh hai số hữu tỉ(07/09)
- Khái niệm về cộng, trừ hai số hữu tỉ(08/09)
- Bài tập về cộng, trừ số hữu tỉ(08/09)
- Lý thuyết về nhân, chia số hữu tỉ(08/09)
- Bài tập về nhân, chia số hữu tỉ(08/09)
- Giá trị tuyệt đối của một số hữu tỉ(09/09)
- Cộng, trừ, nhân, chia số thập phân(10/09)
- Luyện tập: Giá trị tuyệt đối của số hữu tỉ. Cộng, trừ, nhân, chia, số thập phân(10/09)
- Lý thuyết về lũy thừa của một số hữu tỉ(10/09)
chuyên đề được quan tâm
- Chương 1: Khảo sát và vẽ đồ thị hàm số
- Chương 2: Hình học không gian
- Chương 3: Hàm số mũ - hàm số logarit
- Chương 4: Nguyên hàm - tích phân
- Toàn bộ công thức toán học
- Căn bậc hai, Căn bậc ba
- Tổng hợp các đề kiểm tra 1 tiết chương 1...
- Chương 1: Mệnh đề - Tập hợp
- Chương 1: Hàm số lượng giác và phương trình lượng...
- Chương 2: Tổ hợp - xác suất - nhị thức...
bài viết mới nhất
- Các bất đẳng thức THCS cơ bản và nâng cao
- Tính chất ba đường trung tuyến của tam giác (Phần...
- Tính chất ba đường trung tuyến của tam giác (Phần...
- Quan hệ giữa ba cạnh của một tam giác. Bất...
- Quan hệ giữa ba cạnh của một tam giác. Bất...
- Quan hệ giữa ba cạnh của một tam giác. Bất...
- Quan hệ giữa đường vuông góc và đường xiên, đường...
- Quan hệ giữa góc và cạnh đối diện trong một...
- Ôn tập chương 8: Thống kê (Phần 2)
- Ôn tập chương 8: Thống kê (Phần 1)
Cập nhật thông tin mới nhất của kỳ thi tốt nghiệp THPT 2025