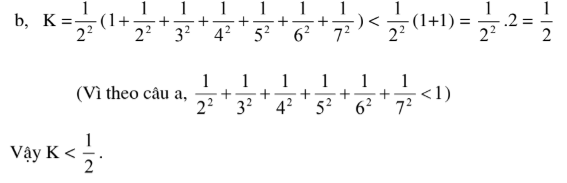Chuyên đề: Lũy thừa của một số hữu tỉ (phần 4)
Cập nhật lúc: 16:17 11-09-2018 Mục tin: LỚP 7
Bài này sẽ giúp các bạn biết được các dạng toán cơ bản về lũy thừa của một số hữu tỉ.
Xem thêm:
Dạng 4: Chứng minh
*) Chứng minh bất đẳng thức:
Bài 1: Chứng minh rằng:
\(\begin{array}{l}a)\,H = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{{2007}^2}}} + \frac{1}{{{{2008}^2}}}\,\, < \,\,1\\b)\,K = \frac{1}{{{2^2}}} + \frac{1}{{{4^2}}} + \frac{1}{{{6^2}}} + \frac{1}{{{8^2}}} + \frac{1}{{{{10}^2}}} + \frac{1}{{{{12}^2}}} + \frac{1}{{{{14}^2}}}\,\, < \,\,\frac{1}{2}\end{array}\)
Giải:
Lưu ý: \(\frac{1}{{n\left( {n + 1} \right)}} = \frac{1}{n} - \frac{1}{{n + 1}}\,\,\,\,\left( {n \in {N^*}} \right)\)
Ta có: \(\frac{1}{{{2^2}}}\,\, < \,\,\frac{1}{{1.2}}\,;\,\,\frac{1}{{{3^2}}}\,\, < \,\,\frac{1}{{2.3}};\,\,\frac{1}{{{4^2}}}\,\, < \,\,\frac{1}{{3.4}};\,.....;\,\,\frac{1}{{{{2008}^2}}}\,\, < \,\,\frac{1}{{2007.2008}}\)
\( \Rightarrow H = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{{2007}^2}}} + \frac{1}{{{{2008}^2}}}\,\,\, < \,\,\,\frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + \,... + \frac{1}{{2006.2007}} + \frac{1}{{2007.2008}}\)
Mà \(\frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + \,... + \frac{1}{{2006.2007}} + \frac{1}{{2007.2008}} = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + ... + \frac{1}{{2006}} - \frac{1}{{2007}} + \frac{1}{{2007}} - \frac{1}{{2008}} = 1 - \frac{1}{{2008}}\,\,\, < \,\,1\)
\( \Rightarrow H\,\, < \,\,1\)
Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:
>> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
- Lý thuyết về số hữu tỉ(07/09)
- So sánh hai số hữu tỉ(07/09)
- Khái niệm về cộng, trừ hai số hữu tỉ(08/09)
- Bài tập về cộng, trừ số hữu tỉ(08/09)
- Lý thuyết về nhân, chia số hữu tỉ(08/09)
- Bài tập về nhân, chia số hữu tỉ(08/09)
- Giá trị tuyệt đối của một số hữu tỉ(09/09)
- Cộng, trừ, nhân, chia số thập phân(10/09)
- Luyện tập: Giá trị tuyệt đối của số hữu tỉ. Cộng, trừ, nhân, chia, số thập phân(10/09)
- Lý thuyết về lũy thừa của một số hữu tỉ(10/09)
chuyên đề được quan tâm
- Chương 1: Khảo sát và vẽ đồ thị hàm số
- Chương 2: Hình học không gian
- Chương 3: Hàm số mũ - hàm số logarit
- Chương 4: Nguyên hàm - tích phân
- Toàn bộ công thức toán học
- Căn bậc hai, Căn bậc ba
- Tổng hợp các đề kiểm tra 1 tiết chương 1...
- Chương 1: Mệnh đề - Tập hợp
- Chương 1: Hàm số lượng giác và phương trình lượng...
- Chương 2: Tổ hợp - xác suất - nhị thức...
bài viết mới nhất
- Các bất đẳng thức THCS cơ bản và nâng cao
- Tính chất ba đường trung tuyến của tam giác (Phần...
- Tính chất ba đường trung tuyến của tam giác (Phần...
- Quan hệ giữa ba cạnh của một tam giác. Bất...
- Quan hệ giữa ba cạnh của một tam giác. Bất...
- Quan hệ giữa ba cạnh của một tam giác. Bất...
- Quan hệ giữa đường vuông góc và đường xiên, đường...
- Quan hệ giữa góc và cạnh đối diện trong một...
- Ôn tập chương 8: Thống kê (Phần 2)
- Ôn tập chương 8: Thống kê (Phần 1)
Cập nhật thông tin mới nhất của kỳ thi tốt nghiệp THPT 2025